- Συγγραφέας Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:35.
- Τελευταία τροποποίηση 2025-06-01 05:04.
Στα στατιστικά, το 68 - 95 - Κανόνας 99,7 , γνωστό και ως εμπειρικό κανόνας , είναι συντομογραφία μεταχειρισμένος να θυμάστε το ποσοστό των τιμών που βρίσκονται μέσα σε μια ζώνη γύρω από το μέσο όρο σε μια κανονική κατανομή με πλάτος δύο, τεσσάρων και έξι τυπικών αποκλίσεων, αντίστοιχα. ακριβέστερα, το 68,27%, το 95,45% και το 99,73% των τιμών βρίσκονται
Από αυτή την άποψη, ποιος είναι ο κανόνας του 95 τοις εκατό;
Το εμπειρικό κανόνας δηλώνει ότι για μια κανονική κατανομή, σχεδόν όλα τα δεδομένα θα εμπίπτουν σε τρεις τυπικές αποκλίσεις του μέσου όρου. 95 % εμπίπτουν σε δύο τυπικές αποκλίσεις. Το 99,7% εμπίπτει σε τρεις τυπικές αποκλίσεις.
Γνωρίζετε επίσης, ποια είναι τα διαστήματα εμπιστοσύνης 68% 95% και 99,7% για τα μέσα του δείγματος; Από 95 % των τιμών εμπίπτουν σε δύο τυπικές αποκλίσεις του σημαίνω σύμφωνα με την 68 - 95 - 99.7 Κανόνα, απλά προσθέστε και αφαιρέστε δύο τυπικές αποκλίσεις από το σημαίνω προκειμένου να αποκτήσετε το 95 % διάστημα εμπιστοσύνης . Σύμφωνα με την 68 - 95 - 99.7 Κανόνας: ➢ Το 68 % διάστημα εμπιστοσύνης για αυτό παράδειγμα είναι μεταξύ 78 και 82.
Επίσης, πρέπει να γνωρίζετε γιατί η τυπική απόκλιση είναι 68 τοις εκατό;
Όπως είπαν άλλοι, είναι αποτέλεσμα του λογισμού ότι αυτός ο τύπος υπολογίστηκε ως ολοκλήρωμα από -1/2 σίγμα έως 1/2 σίγμα (καλύπτοντας 1 σίγμα = 1 τυπική απόκλιση ) προκύπτει ένα εμβαδόν κάτω από την καμπύλη 0,68, με ολόκληρο το εμβαδόν, υπολογισμένο ως αναπόσπαστο από -άπειρο έως +άπειρο να είναι 1, οπότε παίρνετε 68 % Για ένα πρότυπο
Τι είναι το 95 τοις εκατό διάστημα εμπιστοσύνης;
ΕΝΑ 95 % διάστημα εμπιστοσύνης είναι ένα εύρος τιμών που μπορείς να είσαι 95 % ορισμένων περιέχει τον πραγματικό μέσο όρο του πληθυσμού. Με το μικρό δείγμα στα αριστερά, το 95 % διάστημα εμπιστοσύνης είναι παρόμοιο με το εύρος των δεδομένων.
Συνιστάται:
Πώς χρησιμοποιείτε τον κανόνα προϊόντος και πηλίκου;

Ο κανόνας προϊόντος λέει ότι η παράγωγος ενός γινομένου δύο συναρτήσεων είναι η πρώτη συνάρτηση επί την παράγωγο της δεύτερης συνάρτησης συν η δεύτερη συνάρτηση επί την παράγωγο της πρώτης συνάρτησης. Ο κανόνας προϊόντος πρέπει να χρησιμοποιείται όταν πρόκειται να ληφθεί η παράγωγος του πηλίκου δύο συναρτήσεων
Ποια είναι η διαφορά μεταξύ του κανόνα προϊόντος και του κανόνα αλυσίδας;

Χρησιμοποιούμε τον κανόνα της αλυσίδας όταν διαφοροποιούμε μια «συνάρτηση μιας συνάρτησης», όπως η f(g(x)) γενικά. Χρησιμοποιούμε τον κανόνα γινομένου όταν διαφοροποιούμε δύο συναρτήσεις πολλαπλασιασμένες μαζί, όπως η f(x)g(x) γενικά. Αλλά σημειώστε ότι είναι ξεχωριστές λειτουργίες: η μία δεν βασίζεται στην απάντηση στην άλλη
Πώς χρησιμοποιείτε τον κανόνα του δεξιού χεριού για το σταυρωτό προϊόν;
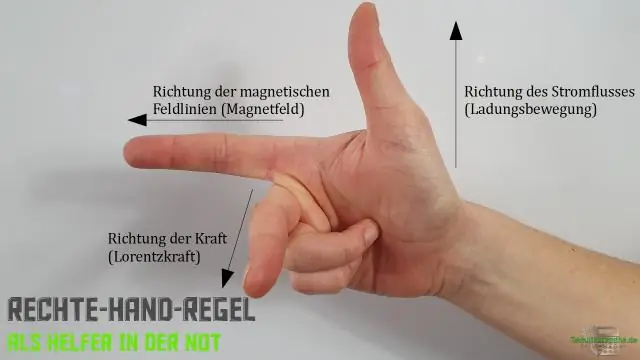
Ο κανόνας του δεξιού χεριού δηλώνει ότι ο προσανατολισμός του διασταυρούμενου γινομένου των διανυσμάτων προσδιορίζεται τοποθετώντας και ουρά προς ουρά, ισοπεδώνοντας το δεξί χέρι, εκτείνοντάς το προς την κατεύθυνση και στη συνέχεια κυρτώνοντας τα δάχτυλα προς την κατεύθυνση που δημιουργεί η γωνία. Στη συνέχεια, ο αντίχειρας δείχνει προς την κατεύθυνση του
Πώς μετατρέπετε τον κανόνα του πηλίκου σε κανόνα προϊόντος;

Ο κανόνας του πηλίκου θα μπορούσε να θεωρηθεί ως εφαρμογή των κανόνων του προϊόντος και της αλυσίδας. Αν Q(x) = f(x)/g(x), τότε Q(x) = f(x) * 1/(g(x)). Μπορείτε να χρησιμοποιήσετε τον κανόνα προϊόντος για να διαφοροποιήσετε το Q(x) και το 1/(g(x)) μπορεί να διαφοροποιηθεί χρησιμοποιώντας τον κανόνα αλυσίδας με u = g(x) και 1/(g(x)) = 1/u
Μπορείτε να χρησιμοποιήσετε τον κανόνα του προϊόντος αντί για τον κανόνα του πηλίκου;

Υπάρχουν δύο λόγοι για τους οποίους ο κανόνας του πηλίκου μπορεί να είναι ανώτερος από τον κανόνα ισχύος συν προϊόντος στη διαφοροποίηση ενός πηλίκου: Διατηρεί κοινούς παρονομαστές όταν απλοποιεί το αποτέλεσμα. Εάν χρησιμοποιείτε τον κανόνα ισχύος συν τον κανόνα προϊόντος, συχνά πρέπει να βρείτε έναν κοινό παρονομαστή για να απλοποιήσετε το αποτέλεσμα
