Βίντεο: Πώς μετατρέπετε τον κανόνα του πηλίκου σε κανόνα προϊόντος;
2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35
ο κανόνας πηλίκου θα μπορούσε να θεωρηθεί ως εφαρμογή του προϊόν και κανόνες αλυσίδας . Αν Q(x) = f(x)/g(x), τότε Q(x) = f(x) * 1/(g(x)). Μπορείτε να χρησιμοποιήσετε το κανόνας προϊόντος για να διαφοροποιηθεί το Q(x) και το 1/(g(x)) μπορεί να διαφοροποιηθεί χρησιμοποιώντας κανόνας της αλυσίδας με u = g(x) και 1/(g(x)) = 1/u.
Επιπλέον, ποιος είναι ο τύπος για τον κανόνα του πηλίκου;
ο κανόνας πηλίκου είναι ένα τύπος για τη λήψη της παραγώγου του α πηλίκο δύο λειτουργιών. ο τύπος δηλώνει ότι για να βρείτε την παράγωγο της f(x) διαιρούμενη με τη g(x), πρέπει: Να πάρετε τη g(x) επί της παραγώγου της f(x). Στη συνέχεια, από αυτό το γινόμενο, πρέπει να αφαιρέσετε το γινόμενο του f(x) επί την παράγωγο του g(x).
Γνωρίζετε επίσης, ποια είναι η παράγωγος του 1; ο Παράγωγο μας λέει την κλίση μιας συνάρτησης σε οποιοδήποτε σημείο. Υπάρχουν κανόνες που μπορούμε να ακολουθήσουμε για να βρούμε πολλούς παράγωγα . Για παράδειγμα: Η κλίση μιας σταθερής τιμής (όπως το 3) είναι πάντα 0.
Παράγωγο Κανόνες.
| Κοινές Λειτουργίες | Λειτουργία | Παράγωγο |
|---|---|---|
| Συνεχής | ντο | 0 |
| Γραμμή | Χ | 1 |
| τσεκούρι | ένα | |
| τετράγωνο | Χ2 | 2x |
Οι άνθρωποι ρωτούν επίσης, ποιος είναι ο κανόνας του προϊόντος και του πηλίκου;
ο Κανόνας προϊόντος λέει ότι η παράγωγος του α προϊόν δύο συναρτήσεων είναι η πρώτη συνάρτηση επί την παράγωγο της δεύτερης συνάρτησης συν η δεύτερη συνάρτηση επί την παράγωγο της πρώτης συνάρτησης.
Ποιος είναι ο κανόνας ισχύος στον λογισμό;
ο κανόνας ισχύος στον λογισμό είναι ένα αρκετά απλό κανόνας που σας βοηθά να βρείτε την παράγωγο μιας μεταβλητής ανυψωμένη σε a εξουσία , όπως: x^5, 2x^8, 3x^(-3) ή 5x^(1/2). Το μόνο που κάνετε είναι να πάρετε τον εκθέτη, να τον πολλαπλασιάσετε με τον συντελεστή (τον αριθμό μπροστά από το x) και να μειώσετε τον εκθέτη κατά 1.
Συνιστάται:
Πώς χρησιμοποιείτε τον κανόνα προϊόντος και πηλίκου;
Ο κανόνας προϊόντος λέει ότι η παράγωγος ενός γινομένου δύο συναρτήσεων είναι η πρώτη συνάρτηση επί την παράγωγο της δεύτερης συνάρτησης συν η δεύτερη συνάρτηση επί την παράγωγο της πρώτης συνάρτησης. Ο κανόνας προϊόντος πρέπει να χρησιμοποιείται όταν πρόκειται να ληφθεί η παράγωγος του πηλίκου δύο συναρτήσεων
Πώς ξέρετε πότε να χρησιμοποιήσετε τον κανόνα του προϊόντος ή του πηλίκου;
Διαίρεση λειτουργιών. Έτσι, κάθε φορά που βλέπετε πολλαπλασιασμό δύο συναρτήσεων, χρησιμοποιήστε τον κανόνα γινομένου και σε περίπτωση διαίρεσης χρησιμοποιήστε τον κανόνα πηλίκου. Εάν η συνάρτηση έχει και πολλαπλασιασμό και διαίρεση, απλώς χρησιμοποιήστε και τους δύο κανόνες ανάλογα. Αν δείτε μια γενική εξίσωση είναι κάτι σαν,, όπου είναι μια συνάρτηση από την άποψη της μόνης
Ποια είναι η διαφορά μεταξύ του κανόνα προϊόντος και του κανόνα αλυσίδας;
Χρησιμοποιούμε τον κανόνα της αλυσίδας όταν διαφοροποιούμε μια «συνάρτηση μιας συνάρτησης», όπως η f(g(x)) γενικά. Χρησιμοποιούμε τον κανόνα γινομένου όταν διαφοροποιούμε δύο συναρτήσεις πολλαπλασιασμένες μαζί, όπως η f(x)g(x) γενικά. Αλλά σημειώστε ότι είναι ξεχωριστές λειτουργίες: η μία δεν βασίζεται στην απάντηση στην άλλη
Πώς χρησιμοποιείτε τον κανόνα του δεξιού χεριού για το σταυρωτό προϊόν;
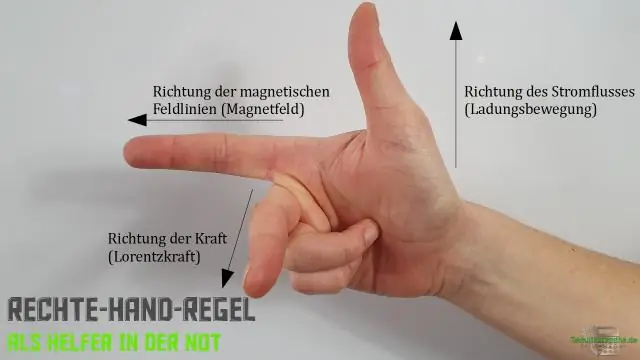
Ο κανόνας του δεξιού χεριού δηλώνει ότι ο προσανατολισμός του διασταυρούμενου γινομένου των διανυσμάτων προσδιορίζεται τοποθετώντας και ουρά προς ουρά, ισοπεδώνοντας το δεξί χέρι, εκτείνοντάς το προς την κατεύθυνση και στη συνέχεια κυρτώνοντας τα δάχτυλα προς την κατεύθυνση που δημιουργεί η γωνία. Στη συνέχεια, ο αντίχειρας δείχνει προς την κατεύθυνση του
Μπορείτε να χρησιμοποιήσετε τον κανόνα του προϊόντος αντί για τον κανόνα του πηλίκου;
Υπάρχουν δύο λόγοι για τους οποίους ο κανόνας του πηλίκου μπορεί να είναι ανώτερος από τον κανόνα ισχύος συν προϊόντος στη διαφοροποίηση ενός πηλίκου: Διατηρεί κοινούς παρονομαστές όταν απλοποιεί το αποτέλεσμα. Εάν χρησιμοποιείτε τον κανόνα ισχύος συν τον κανόνα προϊόντος, συχνά πρέπει να βρείτε έναν κοινό παρονομαστή για να απλοποιήσετε το αποτέλεσμα