Πίνακας περιεχομένων:
Βίντεο: Πώς χρησιμοποιείτε τον κανόνα του δεξιού χεριού για το σταυρωτό προϊόν;
2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35
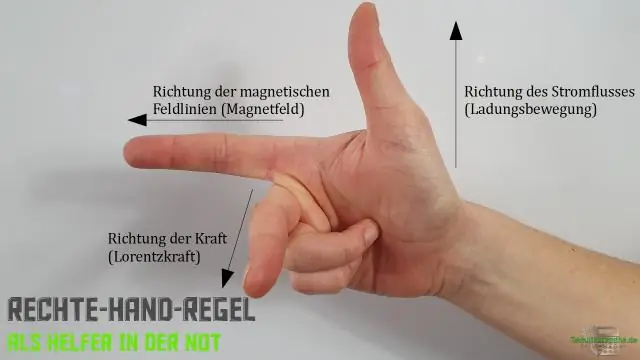
ο σωστά - κανόνας χεριών δηλώνει ότι ο προσανατολισμός των διανυσμάτων σταυρωτό προϊόν καθορίζεται τοποθετώντας και ουρά με ουρά, ισοπεδώνοντας το δεξί χέρι , επεκτείνοντάς το προς την κατεύθυνση του, και στη συνέχεια κυρτώστε τα δάχτυλα προς την κατεύθυνση που κάνει η γωνία με. ο αντίχειρας τότε δείχνει προς την κατεύθυνση του.
Λοιπόν, πώς μπορείτε να κάνετε τον κανόνα του δεξιού χεριού για το σταυρό προϊόν;
ο σταυρωτό προϊόν θα είναι πάντα ένα άλλο διάνυσμα που είναι κάθετο και στα δύο αρχικά διανύσματα. Η κατεύθυνση του σταυρωτό προϊόν βρίσκεται χρησιμοποιώντας το κανόνας του δεξιού χεριού , ενώ το μέγεθος του σταυρωτό προϊόν δίνεται από: Η ροπή είναι η τάση μιας δύναμης να προκαλεί περιστροφή ενός αντικειμένου.
ποιος είναι ο κανόνας cross product; ο σταυρωτό προϊόν Το a × b ορίζεται ως a διάνυσμα c που είναι κάθετο (ορθογώνιο) τόσο στο a όσο και στο b, με κατεύθυνση που δίνεται από το δεξί χέρι κανόνας και μέγεθος ίσο με το εμβαδόν του παραλληλογράμμου που εκτείνονται τα διανύσματα.
Κάποιος μπορεί επίσης να ρωτήσει, πώς χρησιμοποιείτε τον κανόνα του δεξιού χεριού;
Η κατεύθυνση του διασταυρούμενου προϊόντος μπορεί να βρεθεί με την εφαρμογή του κανόνα του δεξιού χεριού ως εξής:
- Ο δείκτης δείχνει προς την κατεύθυνση του διανύσματος ταχύτηταςv.
- Το μεσαίο δάχτυλο δείχνει προς την κατεύθυνση του διανύσματος μαγνητικού πεδίου Β.
- Ο αντίχειρας δείχνει προς την κατεύθυνση του εγκάρσιου γινόμενου F.
Πώς υπολογίζετε το διασταυρούμενο προϊόν;
Μπορούμε υπολογίζω ο Cross Product Έτσι: Το μήκος είναι: το μήκος του a επί του μήκους των b επί το ημίτονο της γωνίας μεταξύ a και b, Στη συνέχεια πολλαπλασιάζουμε με το διάνυσμα n για να βεβαιωθούμε ότι κατευθύνεται προς τη σωστή κατεύθυνση (σε ορθογώνια τόσο στο a όσο και στο b).
Συνιστάται:
Πώς χρησιμοποιείτε τον κανόνα προϊόντος και πηλίκου;
Ο κανόνας προϊόντος λέει ότι η παράγωγος ενός γινομένου δύο συναρτήσεων είναι η πρώτη συνάρτηση επί την παράγωγο της δεύτερης συνάρτησης συν η δεύτερη συνάρτηση επί την παράγωγο της πρώτης συνάρτησης. Ο κανόνας προϊόντος πρέπει να χρησιμοποιείται όταν πρόκειται να ληφθεί η παράγωγος του πηλίκου δύο συναρτήσεων
Πώς χρησιμοποιείτε τον κανόνα 68 95 99;
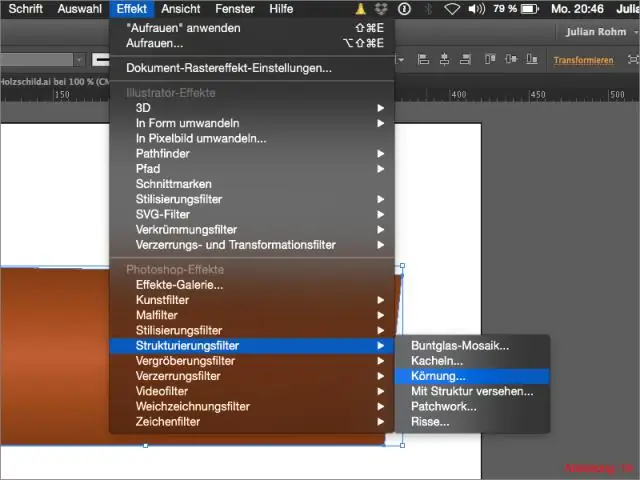
Στις στατιστικές, ο κανόνας 68–95–99,7, γνωστός και ως εμπειρικός κανόνας, είναι μια συντομογραφία που χρησιμοποιείται για να θυμάται το ποσοστό των τιμών που βρίσκονται μέσα σε μια ζώνη γύρω από το μέσο όρο σε μια κανονική κατανομή με πλάτος δύο, τεσσάρων και έξι προτύπων αποκλίσεις, αντίστοιχα. ακριβέστερα, το 68,27%, το 95,45% και το 99,73% των τιμών βρίσκονται
Ποια είναι η διαφορά μεταξύ του κανόνα προϊόντος και του κανόνα αλυσίδας;
Χρησιμοποιούμε τον κανόνα της αλυσίδας όταν διαφοροποιούμε μια «συνάρτηση μιας συνάρτησης», όπως η f(g(x)) γενικά. Χρησιμοποιούμε τον κανόνα γινομένου όταν διαφοροποιούμε δύο συναρτήσεις πολλαπλασιασμένες μαζί, όπως η f(x)g(x) γενικά. Αλλά σημειώστε ότι είναι ξεχωριστές λειτουργίες: η μία δεν βασίζεται στην απάντηση στην άλλη
Πώς μετατρέπετε τον κανόνα του πηλίκου σε κανόνα προϊόντος;
Ο κανόνας του πηλίκου θα μπορούσε να θεωρηθεί ως εφαρμογή των κανόνων του προϊόντος και της αλυσίδας. Αν Q(x) = f(x)/g(x), τότε Q(x) = f(x) * 1/(g(x)). Μπορείτε να χρησιμοποιήσετε τον κανόνα προϊόντος για να διαφοροποιήσετε το Q(x) και το 1/(g(x)) μπορεί να διαφοροποιηθεί χρησιμοποιώντας τον κανόνα αλυσίδας με u = g(x) και 1/(g(x)) = 1/u
Μπορείτε να χρησιμοποιήσετε τον κανόνα του προϊόντος αντί για τον κανόνα του πηλίκου;
Υπάρχουν δύο λόγοι για τους οποίους ο κανόνας του πηλίκου μπορεί να είναι ανώτερος από τον κανόνα ισχύος συν προϊόντος στη διαφοροποίηση ενός πηλίκου: Διατηρεί κοινούς παρονομαστές όταν απλοποιεί το αποτέλεσμα. Εάν χρησιμοποιείτε τον κανόνα ισχύος συν τον κανόνα προϊόντος, συχνά πρέπει να βρείτε έναν κοινό παρονομαστή για να απλοποιήσετε το αποτέλεσμα