
- Συγγραφέας Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:35.
- Τελευταία τροποποίηση 2025-06-01 05:04.
Τετραγωνικές συναρτήσεις μπορεί να αναπαρασταθεί συμβολικά από το εξίσωση , y(x) = τσεκούρι2 + bx + c, όπου τα a, b και c είναι σταθερές, και a ≠ 0. Αυτή η μορφή αναφέρεται ως τυπική μορφή.
Οι άνθρωποι ρωτούν επίσης, ποια είναι η συμβολική αναπαράσταση μιας συνάρτησης;
Λειτουργίες . Ίσως είστε πιο εξοικειωμένοι με το συμβολική αναπαράσταση του λειτουργίες , όπως η εξίσωση, y = f(x). Λειτουργίες μπορεί να αναπαρασταθεί με πίνακες, σύμβολα , ή γραφήματα.
Ομοίως, πώς προσδιορίζετε το σχήμα ενός τετραγωνικού γραφήματος; Το σχήμα της παραβολής
- Αν a>0, τότε η παραβολή έχει ελάχιστο σημείο και ανοίγει προς τα πάνω (σε σχήμα U) π.χ.
- Αν a<0, τότε η παραβολή έχει μέγιστο σημείο και ανοίγει προς τα κάτω (σε σχήμα ν) π.χ.
- (α) Ελέγξτε εάν a>0 ή a<0 για να αποφασίσετε αν έχει σχήμα U ή n.
- (γ) Οι συντεταγμένες της τομής y (υποκατάστατο x=0).
Κατά συνέπεια, πώς αντιπροσωπεύετε μια τετραγωνική συνάρτηση;
Γραφικές παραστάσεις. ΕΝΑ τετραγωνική λειτουργία είναι μία από τη μορφή f(x) = ax2 + bx + c, όπου τα a, b και c είναι αριθμοί με a όχι ίσο με μηδέν. Η γραφική παράσταση του α τετραγωνική λειτουργία είναι μια καμπύλη που ονομάζεται παραβολή. Οι παραβολές μπορεί να ανοίγουν προς τα πάνω ή προς τα κάτω και να ποικίλλουν σε "πλάτος" ή "απότομο", αλλά όλες έχουν το ίδιο βασικό σχήμα "U".
Πώς λύνεις μια συνάρτηση;
Για λειτουργίες , οι δύο συμβολισμοί σημαίνουν ακριβώς το ίδιο πράγμα, αλλά το "f (x)" σας δίνει μεγαλύτερη ευελιξία και περισσότερες πληροφορίες. Έλεγες "y = 2x + 3; λύσει για y όταν x = -1". Τώρα λέτε "f (x) = 2x + 3; βρείτε f (-1)" (προφέρεται ως "f-of-x ισούται με 2x συν τρία, βρείτε f-of-negative-one").
Συνιστάται:
Πώς βρίσκετε τη δεύτερη παράγωγο μιας συνάρτησης trig;
ΒΙΝΤΕΟ Λοιπόν, ποιες είναι οι παράγωγοι των 6 συναρτήσεων trig; Παράγωγοι Τριγωνομετρικών Συναρτήσεων. Οι βασικές τριγωνομετρικές συναρτήσεις περιλαμβάνουν τις ακόλουθες 6 συναρτήσεις: ημιτόνου ( αμαρτία x), συνημίτονο ( cos x), εφαπτομένη (tanx), συνεφαπτομένη (cotx), secant (secx) και cosecant (cscx).
Πώς βρίσκετε τη συχνότητα κατωφλίου μιας συνάρτησης εργασίας;

Για να το υπολογίσετε αυτό, θα χρειαστείτε την ενέργεια του φωτός που προσπίπτει στο υλικό και την κινητική ενέργεια του φωτοηλεκτρονίου που εκτοξεύεται. Χρησιμοποιώντας E = hf μπορούμε να υπολογίσουμε τη συχνότητα του φωτός υποβαίνοντας στην ενέργεια και υπολογίζοντας για f. Αυτή θα είναι η συχνότητα κατωφλίου
Πώς βρίσκετε τη μέγιστη τιμή μιας τετραγωνικής συνάρτησης;

Εάν σας δοθεί ο τύπος y = ax2 + bx + c, τότε μπορείτε να βρείτε τη μέγιστη τιμή χρησιμοποιώντας τον τύπο max =c- (b2 / 4a). Εάν έχετε την εξίσωση y = a(x-h)2 + k και το θέατρο είναι αρνητικό, τότε η μέγιστη τιμή είναι k
Πώς βρίσκετε το πεδίο ορισμού μιας αλγεβρικής συνάρτησης;
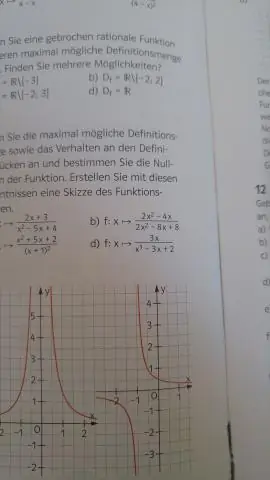
Ο τομέας μιας συνάρτησης είναι το σύνολο όλων των πιθανών εισόδων για τη συνάρτηση. Για παράδειγμα, το πεδίο ορισμού του f(x)=x² είναι όλοι οι πραγματικοί αριθμοί και το πεδίο ορισμού του g(x)=1/x είναι όλοι οι πραγματικοί αριθμοί εκτός από τον x=0
Ποια είναι η συμβολική αναπαράσταση μιας συνάρτησης;

Λειτουργίες. Ίσως είστε πιο εξοικειωμένοι με τη συμβολική αναπαράσταση συναρτήσεων, όπως η εξίσωση, y = f(x). Οι συναρτήσεις μπορούν να αναπαρασταθούν με πίνακες, σύμβολα ή γραφήματα
