Πίνακας περιεχομένων:
- Συγγραφέας Miles Stephen [email protected].
- Public 2023-12-15 23:35.
- Τελευταία τροποποίηση 2025-01-22 16:57.
Αξιολόγηση σύνθετων συναρτήσεων με χρήση γραφημάτων
- Εντοπίστε τη δεδομένη είσοδο στο εσωτερικό λειτουργία στον άξονα x της γραφικής του παράστασης.
- Διαβάστε την έξοδο του εσωτερικού λειτουργία από τον άξονα y της γραφικής του παράστασης.
- Εντοπίστε το εσωτερικό λειτουργία έξοδο στον άξονα x της γραφικής παράστασης του εξωτερικού λειτουργία .
Εδώ, πώς γράφετε και αξιολογείτε τις σύνθετες συναρτήσεις;
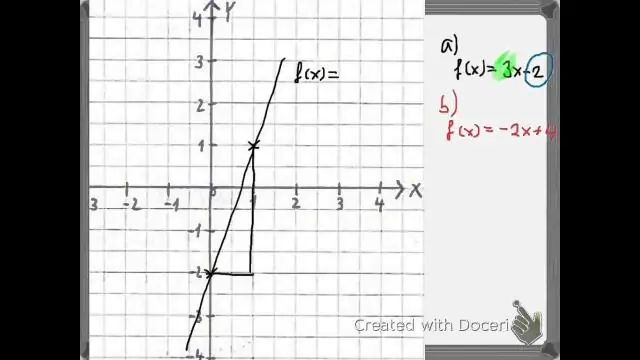
Να κάνει ένα σύνθετη συνάρτηση όπου βάζουμε g(x) μέσα στο λειτουργία f(x), μπορούμε γράφω αυτό f(g(x)). Παρατηρήστε ότι αντί να βάλετε απλώς ένα x στο λειτουργία , αντικαθιστούμε ολόκληρο το g(x) λειτουργία . Όταν το κάνουμε αυτό, έχουμε f(g(x)) = (3x) + 2. Στα αριστερά, θα δείτε ότι το g λειτουργία είναι μέσα στο στ λειτουργία.
Ομοίως, τι είναι ένα παράδειγμα σύνθετης συνάρτησης; ΕΝΑ σύνθετη συνάρτηση είναι ένα λειτουργία αυτό εξαρτάται από άλλον λειτουργία . ΕΝΑ σύνθετη συνάρτηση δημιουργείται όταν ένα λειτουργία αντικαθίσταται με άλλο λειτουργία . Για παράδειγμα , f(g(x)) είναι το σύνθετη συνάρτηση που σχηματίζεται όταν το g(x) αντικαθιστά το x σε f(x). Στο σύνθεση (f ο g)(x), το πεδίο ορισμού της f γίνεται g(x).
Οι άνθρωποι ρωτούν επίσης, ποια είναι τα βήματα για την επίλυση μιας σύνθετης συνάρτησης;
Εδώ είναι τα βήματα μπορούμε να χρησιμοποιήσουμε για να βρούμε το σύνθεση από δύο λειτουργίες : Βήμα 1: Ξαναγράψτε το σύνθεση σε διαφορετική μορφή. Για παράδειγμα, το σύνθεση (f g)(x) πρέπει να ξαναγραφτεί ως f(g(x)). Βήμα 2: Αντικαταστήστε κάθε εμφάνιση του x που βρίσκεται στο εξωτερικό λειτουργία με το εσωτερικό λειτουργία.
Τι σημαίνει σύνθετη συνάρτηση;
: ένα λειτουργία των οποίων οι τιμές βρίσκονται από δύο δεδομένες λειτουργίες εφαρμόζοντας ένα λειτουργία σε μια ανεξάρτητη μεταβλητή και στη συνέχεια εφαρμόζοντας τη δεύτερη λειτουργία στο αποτέλεσμα και του οποίου ο τομέας αποτελείται από εκείνες τις τιμές της ανεξάρτητης μεταβλητής για τις οποίες το αποτέλεσμα προέκυψε από την πρώτη λειτουργία βρίσκεται στον τομέα του δεύτερου.
Συνιστάται:
Πώς πολλαπλασιάζεις τις σύνθετες συναρτήσεις;

Πολλαπλασιασμός και σύνθεση συναρτήσεων Για να πολλαπλασιάσετε μια συνάρτηση με ένα βαθμωτό, πολλαπλασιάστε κάθε έξοδο με αυτόν τον βαθμωτό. Όταν παίρνουμε την f (g(x)), λαμβάνουμε την g(x) ως είσοδο της συνάρτησης f. Για παράδειγμα, αν f (x) = 10x και g(x) = x + 1, τότε για να βρούμε τη f (g(4)), βρίσκουμε g(4) = 4 + 1 + 5 και στη συνέχεια αξιολογούμε την f (5 ) = 10(5) = 50. Παράδειγμα: f (x) = 2x - 2, g(x) = x2 - 8
Πώς βρίσκετε τις συναρτήσεις trig τόξου;

Συμβολίζουμε την αντίστροφη συνάρτηση ως y=sin−1(x). Διαβάζεται το y είναι το αντίστροφο του ημιτόνου x και σημαίνει ότι το y είναι η γωνία πραγματικού αριθμού της οποίας η τιμή του ημιτόνου είναι x. Προσέξτε τη σημειογραφία που χρησιμοποιείται. Γραφήματα Αντίστροφων Τριγωνομετρικών Συναρτήσεων. Εύρος τομέα συνάρτησης csc−1(x) (&μείον;∞,&μείον;1]&κύπελλο;[1,∞) [&μείον;π2,0)∪(0,π2]
Γιατί οι τριγωνομετρικές συναρτήσεις ονομάζονται κυκλικές συναρτήσεις;

Οι τριγωνομετρικές συναρτήσεις μερικές φορές ονομάζονται κυκλικές συναρτήσεις. Αυτό συμβαίνει επειδή οι δύο θεμελιώδεις τριγωνομετρικές συναρτήσεις – το ημίτονο και το συνημίτονο – ορίζονται ως οι συντεταγμένες ενός σημείου P που ταξιδεύει γύρω από τον κύκλο μονάδας της ακτίνας 1. Το ημίτονο και το συνημίτονο επαναλαμβάνουν τις εξόδους τους σε τακτά διαστήματα
Πώς γράφετε τις λογαριθμικές συναρτήσεις σε μια αριθμομηχανή;

Στην αριθμομηχανή γραφημάτων, ο λογάριθμος βάσης e είναι το κλειδί ln. Και τα τρία είναι ίδια. Εάν έχετε τη συνάρτηση logBASE, μπορεί να χρησιμοποιηθεί για την εισαγωγή της συνάρτησης (δείτε στο Y1 παρακάτω). Εάν όχι, χρησιμοποιήστε τον τύπο αλλαγής βάσης (δείτε στο Y2 παρακάτω)
Πώς μετασχηματίζετε τις γραμμικές συναρτήσεις;
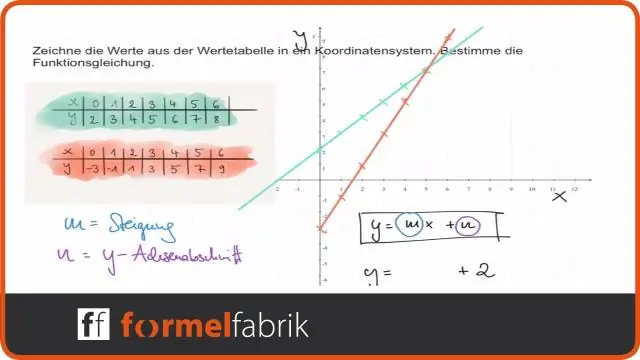
Πώς να: Δεδομένης της εξίσωσης μιας γραμμικής συνάρτησης, χρησιμοποιήστε μετασχηματισμούς για να γράψετε τη γραμμική συνάρτηση με τη μορφή f(x)=mx+b f (x) = m x + b. Γράφημα f(x)=x f (x) = x. Τεντώστε κατακόρυφα ή συμπιέστε το γράφημα κατά έναν παράγοντα |m|. Μετατοπίστε το γράφημα προς τα πάνω ή προς τα κάτω b μονάδες
