Βίντεο: Πώς βρίσκετε τους περιορισμούς μιας ορθολογικής έκφρασης;
2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35
ο περιορισμός είναι ότι ο παρονομαστής δεν μπορεί να είναι ίσος με μηδέν. Άρα σε αυτό το πρόβλημα, αφού το 4x είναι στον παρονομαστή δεν μπορεί να ισούται με μηδέν. Βρείτε όλες τις τιμές του x που σας δίνουν μηδέν στον παρονομαστή. Για να βρείτε το περιορισμούς πάνω σε λογικός συνάρτηση, βρείτε τις τιμές της μεταβλητής που κάνουν τον παρονομαστή ίσο με 0.
Με αυτόν τον τρόπο, μπορεί μια ορθολογική έκφραση να μην έχει περιορισμούς;
Λοιπόν το ίδιο είναι αλήθεια για ορθολογικές εκφράσεις . Το δεύτερο ορθολογική έκφραση είναι ποτέ μηδέν στον παρονομαστή και έτσι δεν το κάνουμε χρειάζομαι να ανησυχείς τυχόν περιορισμούς . Σημειώστε επίσης ότι ο αριθμητής του δεύτερου ορθολογική έκφραση βούληση να είναι μηδέν. Οτι είναι εντάξει, εμείς απλά χρειάζομαι για να αποφευχθεί η διαίρεση με το μηδέν.
Εκτός από τα παραπάνω, πώς λύνεις ορθολογικές εκφράσεις; Τα βήματα για την επίλυση μιας ορθολογικής εξίσωσης είναι:
- Βρείτε τον κοινό παρονομαστή.
- Πολλαπλασιάστε τα πάντα με τον κοινό παρονομαστή.
- Απλοποιώ.
- Ελέγξτε τις απαντήσεις για να βεβαιωθείτε ότι δεν υπάρχει εξωγενής λύση.
Δεύτερον, γιατί δηλώνουμε περιορισμούς για ορθολογική έκφραση και πότε δηλώνουμε τους περιορισμούς;
Απάντηση Επαληθεύτηκε από εμπειρογνώμονα Ορθολογικές εκφράσεις είναι αυτά που έχουν κλασματικούς όρους. Δηλώνουμε περιορισμούς γιατί μπορεί να κάνει την εξίσωση να είναι απροσδιόριστος σε ορισμένες τιμές του x. Η πιο κοινή περιορισμός για ορθολογικές εκφράσεις είναι N/0. Αυτό σημαίνει ότι οποιοσδήποτε αριθμός διαιρούμενος με το μηδέν είναι απροσδιόριστος.
Πώς λύνεις ορθολογικές αλγεβρικές εκφράσεις;
- Λύση:
- Βήμα 1: Προσδιορίστε όλους τους παρονομαστές και προσδιορίστε την οθόνη LCD.
- Βήμα 2: Προσδιορίστε τους περιορισμούς. Στην περίπτωση αυτή, είναι x≠−2 x ≠ − 2 και x≠−3 x ≠ − 3.
- Βήμα 3: Πολλαπλασιάστε και τις δύο πλευρές της εξίσωσης με την οθόνη LCD.
- Βήμα 4: Λύστε την εξίσωση που προκύπτει.
- Βήμα 5: Ελέγξτε για εξωτερικές λύσεις.
Συνιστάται:
Γιατί δηλώνουμε περιορισμούς για ορθολογική έκφραση και πότε δηλώνουμε τους περιορισμούς;
Δηλώνουμε περιορισμούς γιατί μπορεί η εξίσωση να είναι απροσδιόριστος σε ορισμένες τιμές του x. Ο πιο συνηθισμένος περιορισμός για ορθολογικές εκφράσεις είναι N/0. Αυτό σημαίνει ότι οποιοσδήποτε αριθμός διαιρούμενος με το μηδέν είναι απροσδιόριστος. Για παράδειγμα, για τη συνάρτηση f(x) = 6/x², όταν αντικαθιστάτε το x=0, θα έχει ως αποτέλεσμα 6/0 το οποίο είναι απροσδιόριστο
Ποιο είναι το προϊόν μιας έκφρασης;
Στα μαθηματικά, ένα γινόμενο είναι το αποτέλεσμα πολλαπλασιασμού ή μια έκφραση που προσδιορίζει παράγοντες που πρέπει να πολλαπλασιαστούν. Έτσι, για παράδειγμα, το 15 είναι το γινόμενο του 3 και του 5 (το αποτέλεσμα του πολλαπλασιασμού) και είναι το γινόμενο του και (που δείχνει ότι οι δύο παράγοντες πρέπει να πολλαπλασιαστούν μαζί)
Ποια πρόταση περιγράφει καλύτερα τις εξαιρούμενες τιμές μιας ορθολογικής έκφρασης;
Η εξαιρούμενη τιμή μιας ορθολογικής παράστασης είναι οι τιμές όπου ο παρονομαστής της παράστασης είναι μηδέν. Επίσης, ο αριθμός των μηδενικών ενός πολυωνύμου είναι πάντα μικρότερος ή ίσος με τον βαθμό του πολυωνύμου. Επομένως, ο αριθμός των εξαιρούμενων τιμών μιας ορθολογικής παράστασης δεν μπορεί να υπερβαίνει τον βαθμό του παρονομαστή
Τι σημαίνει συμπύκνωση μιας λογαριθμικής έκφρασης;
Μια λογαριθμική έκφραση είναι μια έκφραση που περιέχει λογάριθμους. Για να συμπυκνώσετε λογαριθμικές εκφράσεις σημαίνει να χρησιμοποιήσετε τους λογαριθμικούς νόμους για να μειώσετε τις λογαριθμικές εκφράσεις από τη διευρυμένη μορφή σε μια συμπυκνωμένη μορφή. Η γνώση των νόμων/ιδιοτήτων του λογαρίθμου θα είναι σημαντική για τη συμπύκνωση λογαριθμικών εκφράσεων
Ποια είναι τα βήματα στον πολλαπλασιασμό της ορθολογικής αλγεβρικής έκφρασης;
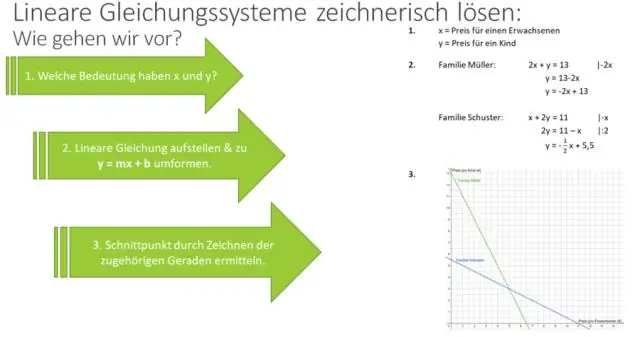
Τα Q και S δεν είναι ίσα με 0. Βήμα 1: Συντελεστής και ο αριθμητής και ο παρονομαστής. Βήμα 2: Γράψτε ως ένα κλάσμα. Βήμα 3: Απλοποιήστε τη λογική έκφραση. Βήμα 4: Πολλαπλασιάστε τους υπόλοιπους παράγοντες στον αριθμητή ή/και στον παρονομαστή. Βήμα 1: Συντελεστής και ο αριθμητής και ο παρονομαστής. Βήμα 2: Γράψτε ως ένα κλάσμα