Πίνακας περιεχομένων:
Βίντεο: Πώς βρίσκετε την εξίσωση μιας ευθείας με ένα σημείο και μια παράλληλη ευθεία;
2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35
ο εξίσωση απο γραμμή στη μορφή κλίσης-τομής είναι y=2x+5. Η κλίση του παράλληλη είναι το ίδιο: m=2. Ετσι το εξίσωση απο παράλληλη γραμμή είναι y=2x+a. Για να βρούμε το α, χρησιμοποιούμε το γεγονός ότι το γραμμή πρέπει να περάσει μέσα από το δεδομένο σημείο :5=(2)⋅(−3)+a.
Ξέρετε επίσης, πώς βρίσκετε την εξίσωση μιας παράλληλης ευθείας που διέρχεται από ένα δεδομένο σημείο;
Μέθοδος 1: Χρήση φόρμας τομής κλίσης
- Αντικαταστήστε την κλίση από την αρχική γραμμή (3 σε αυτήν την περίπτωση) στην εξίσωση της ευθείας y = 3x + b.
- Αντικαταστήστε το δεδομένο σημείο (1, 7) με τις τιμές x και y 7 =3(1) + b.
- Λύστε για το b (την τομή y)
- Αντικαταστήστε αυτήν την τιμή με το 'b' στην εξίσωση τομής κλίσης y = 3x + 4.
Επιπλέον, πώς γράφετε την εξίσωση μιας ευθείας μέσα από ένα σημείο; ο εξίσωση μιας γραμμής τυπικά γράφεται asy=mx+b όπου m είναι η κλίση και b η τομή y. Εάν α σημείο ότι ένα γραμμή περνάει διά μέσου , και την κλίση της, αυτή η σελίδα θα σας δείξει πώς να το βρείτε εξίσωση απο γραμμή . Γέμισε το σημείο ότι η γραμμή περνάει διά μέσου
Επιπλέον, πώς βρίσκω την εξίσωση μιας παράλληλης ευθείας;
Δύο γραμμές είναι παράλληλο εάν έχουν την ίδια κλίση. Παράδειγμα 1: Εύρημα η κλίση του παράλληλη γραμμή στο γραμμή 4x – 5y = 12. Προς εύρημα η κλίση αυτού γραμμή πρέπει να πάρουμε το γραμμή μορφή inslope-intercept (y = mx + b), που σημαίνει ότι πρέπει να λύσουμε το fory: Η κλίση του γραμμή 4x – 5y = 12 είναι m =4/5.
Πώς κατασκευάζετε μια ευθεία παράλληλη σε μια δεδομένη ευθεία;
Μέθοδος 1 Σχεδίαση κάθετων γραμμών
- Εντοπίστε τη δεδομένη ευθεία και το δεδομένο σημείο.
- Σχεδιάστε ένα τόξο που τέμνει τη δεδομένη ευθεία σε δύο διαφορετικά σημεία.
- Σχεδιάστε ένα μικρό τόξο απέναντι από το δεδομένο σημείο.
- Σχεδιάστε ένα άλλο μικρό τόξο που τέμνει το προηγούμενο.
Συνιστάται:
Πώς βρίσκετε την εξίσωση μιας ευθείας κάθετης σε ένα σημείο;
Πρώτα, βάλτε την εξίσωση της γραμμής που δίνεται σε μορφή κλίσης-τομής λύνοντας το y. Παίρνετε y = 2x +5, οπότε η κλίση είναι –2. Οι κάθετες γραμμές έχουν αντίθετες-αντίστροφες κλίσεις, άρα η κλίση της ευθείας που θέλουμε να βρούμε είναι 1/2. Βάζοντας το σημείο που δίνεται στην εξίσωση y = 1/2x + b και λύνοντας το b, παίρνουμε b =6
Ποιο είναι το πρώτο βήμα για την κατασκευή μιας κάθετης από ένα σημείο σε μια ευθεία;
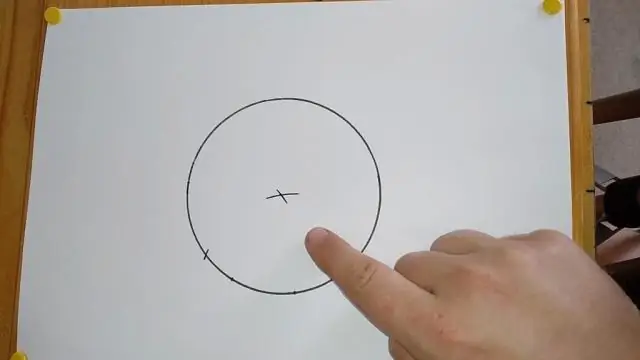
Συνδέστε το δεδομένο σημείο στο σημείο όπου τέμνονται τα τόξα. Χρησιμοποιήστε ένα ίσιο για να βεβαιωθείτε ότι η γραμμή είναι ευθεία. Η ευθεία που σχεδιάζετε είναι κάθετη στην πρώτη γραμμή, μέσα από το δεδομένο σημείο στη γραμμή
Θα είχε νόημα να βρούμε την εξίσωση μιας ευθείας παράλληλης σε μια δεδομένη ευθεία και μέσω ενός σημείου στη δεδομένη ευθεία;
Η εξίσωση μιας ευθείας που είναι παράλληλη ή κάθετη σε μια δεδομένη ευθεία; Πιθανή απάντηση: Οι κλίσεις των παράλληλων ευθειών είναι ίσες. Αντικαταστήστε τη γνωστή κλίση και τις συντεταγμένες ενός σημείου στην άλλη ευθεία στη μορφή κλίσης σημείου για να βρείτε την εξίσωση της παράλληλης ευθείας
Πώς βρίσκετε την κλίση μιας παράλληλης και κάθετης ευθείας;
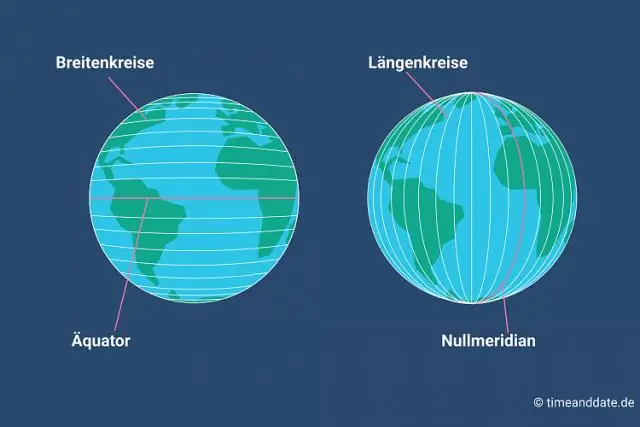
Για να βρούμε την κλίση αυτής της γραμμής πρέπει να βάλουμε τη γραμμή σε μορφή κλίσης-τομής (y = mx + b), που σημαίνει ότι πρέπει να λύσουμε για το y: Η κλίση της γραμμής 4x – 5y = 12 είναι m = 4/ 5. Επομένως, η κλίση κάθε ευθείας παράλληλης σε αυτήν την ευθεία θα πρέπει να είναι m = 4/5. Δύο ευθείες είναι κάθετες αν
Πώς βρίσκετε την εξίσωση μιας υπερβολής με ασύμπτωτες και εστίες;
Χρησιμοποιώντας τον παραπάνω συλλογισμό, οι εξισώσεις των ασυμπτωμάτων είναι y=±ab(x−h)+k y = ± a b (x −h) + k. Όπως οι υπερβολές με κέντρο στην αρχή, οι υπερβολές με κέντρο σε ένα σημείο (h,k) έχουν κορυφές, συν-κορυφές και εστίες που σχετίζονται με την εξίσωση c2=a2+b2 c 2 = a 2 + b 2