Μπορεί το ολοκληρωμένο τεστ να αποδείξει απόκλιση;
Μπορεί το ολοκληρωμένο τεστ να αποδείξει απόκλιση;

Βίντεο: Μπορεί το ολοκληρωμένο τεστ να αποδείξει απόκλιση;

Βίντεο: Μπορεί το ολοκληρωμένο τεστ να αποδείξει απόκλιση;
Βίντεο: Ψυχανάλυση Κρυπτοαγορών #76 2024, Ενδέχεται
Anonim

Παράδειγμα 1 Προσδιορίστε εάν η ακόλουθη σειρά είναι συγκλίνουσα ή αποκλίνων . Αυτή η συνάρτηση είναι σαφώς θετική και αν κάνουμε x x μεγαλύτερο τον παρονομαστή θα μεγαλώνουν και έτσι η συνάρτηση μειώνεται επίσης. ο αναπόσπαστο είναι αποκλίνων και έτσι είναι και η σειρά αποκλίνων από το Ολοκληρωμένη δοκιμή.

Εκτός από αυτό, το e x είναι συγκλίνον ή αποκλίνον;

1/( πρώην ) είναι μεγαλύτερο ή ίσο με 1/( πρώην +1) (μεταξύ μηδέν και άπειρου) Λανθασμένο ολοκλήρωμα ∫∞01( πρώην )ρε Χ είναι συγκεντρούμενος και είναι 1 ωστόσο, ακατάλληλο ολοκλήρωμα ∫∞01( πρώην +1)δ Χ είναι αποκλίνων.

Μπορεί επίσης να ρωτήσει κανείς, τι είναι το ακατάλληλο ολοκλήρωμα με το παράδειγμα; Ενα ακατάλληλο ολοκλήρωμα είναι σίγουρη αναπόσπαστο που έχει ένα ή και τα δύο όρια άπειρο ή ένα ολοκλήρωμα που πλησιάζει το άπειρο σε ένα ή περισσότερα σημεία του εύρους ολοκλήρωσης. Ακατάλληλα ολοκληρώματα δεν μπορεί να υπολογιστεί χρησιμοποιώντας έναν κανονικό Riemann αναπόσπαστο . Για παράδειγμα , ο αναπόσπαστο.

Δεύτερον, τι είναι η σύγκλιση και η απόκλιση στον λογισμό;

Σειρά Σύγκλιση και Απόκλιση - Ορισμοί Α σειρά Σa συγκλίνει σε ένα άθροισμα S εάν και μόνο αν η ακολουθία των μερικών αθροισμάτων συγκλίνει στο S. Δηλαδή, μια σειρά συγκλίνει εάν υπάρχει το ακόλουθο όριο: Διαφορετικά, εάν το όριο του sκ (καθώς το k → ∞) είναι άπειρο ή δεν υπάρχει, τότε η σειρά αποκλίνει.

Ποια είναι η τιμή του 1 άπειρου;

Ουσιαστικά, 1 διαιρούμενος με έναν πολύ μεγάλο αριθμό πλησιάζει πολύ το μηδέν, οπότε… 1 διαιρείται με άπειρο , αν μπορούσατε πραγματικά να φτάσετε άπειρο , ισούται με 0.

Συνιστάται:

Πώς υπολογίζετε την τυπική απόκλιση από το PMP;

Πώς υπολογίζετε την τυπική απόκλιση από το PMP;

Ο τύπος που χρησιμοποιείται στο PMBOK για την τυπική απόκλιση είναι απλός. Είναι απλώς (P-O)/6. Αυτή είναι η απαισιόδοξη εκτίμηση δραστηριότητας μείον την αισιόδοξη εκτίμηση δραστηριότητας διαιρούμενη με έξι. Το πρόβλημα είναι ότι αυτό σε καμία περίπτωση το σχήμα ή η μορφή δεν παράγει ένα μέτρο τυπικής απόκλισης

Με τι χρησιμοποιείται η τυπική απόκλιση σε συνδυασμό;

Με τι χρησιμοποιείται η τυπική απόκλιση σε συνδυασμό;

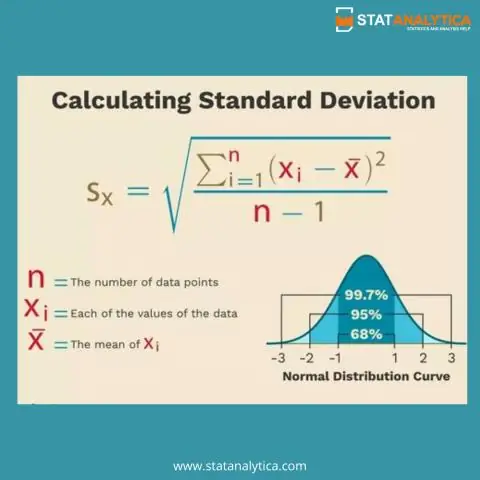
Η τυπική απόκλιση χρησιμοποιείται σε συνδυασμό με το MEAN για να περιγράψει αριθμητικά τις κατανομές που έχουν σχήμα καμπάνας. Το MEAN μετρά το κέντρο του; κατανομή, ενώ η τυπική απόκλιση μετρά την ΕΞΑΠΛΩΣΗ της διανομής

Πώς υπολογίζετε την τυπική απόκλιση στην ΠΧΠ;

Πώς υπολογίζετε την τυπική απόκλιση στην ΠΧΠ;

Υπολογισμός της τυπικής απόκλισης Υπολογισμός του μέσου όρου της διεργασίας μ Αφαιρέστε τον μέσο όρο της διεργασίας από κάθε μετρούμενη τιμή δεδομένων (οι τιμές X i) Τετράγωνο καθεμίας από τις αποκλίσεις που υπολογίστηκαν στο βήμα 2. Προσθέστε όλες τις τετραγωνικές αποκλίσεις που υπολογίστηκαν στο βήμα 3. Διαιρέστε το αποτέλεσμα βήμα 4 από το μέγεθος του δείγματος

Ποια απόδειξη χρησιμοποιεί σχήματα σε επίπεδο συντεταγμένων για να αποδείξει γεωμετρικές ιδιότητες;

Ποια απόδειξη χρησιμοποιεί σχήματα σε επίπεδο συντεταγμένων για να αποδείξει γεωμετρικές ιδιότητες;

Μια απόδειξη που χρησιμοποιεί σχήματα σε επίπεδο συντεταγμένων για να αποδείξει γεωμετρικές ιδιότητες αναφέρεται ως τριγωνομετρική

Ποια είναι η διαφορά μεταξύ ενός τεστ t ζεύξης και ενός τεστ t 2 δειγμάτων;

Ποια είναι η διαφορά μεταξύ ενός τεστ t ζεύξης και ενός τεστ t 2 δειγμάτων;

Το τεστ t δύο δειγμάτων χρησιμοποιείται όταν τα δεδομένα δύο δειγμάτων είναι στατιστικά ανεξάρτητα, ενώ το ζευγοποιημένο t-test χρησιμοποιείται όταν τα δεδομένα έχουν τη μορφή ταιριασμένων ζευγών. Για να χρησιμοποιήσουμε το τεστ t δύο δειγμάτων, πρέπει να υποθέσουμε ότι τα δεδομένα και από τα δύο δείγματα είναι κανονικά κατανεμημένα και έχουν τις ίδιες διακυμάνσεις