Πίνακας περιεχομένων:
Βίντεο: Πώς βρίσκετε τις ρίζες μιας εξίσωσης αλγεβρικά;
2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35
ο ρίζες οποιουδήποτε τετραγωνικού εξίσωση δίνεται από: x = [-b +/- sqrt(-b^2 - 4ac)]/2a. Γράψτε το τετράγωνο με τη μορφή ax^2 + bx + c = 0. Αν το εξίσωση έχει τη μορφή y = ax^2 + bx +c, απλώς αντικαταστήστε το y με 0. Αυτό γίνεται επειδή το ρίζες απο εξίσωση είναι οι τιμές όπου ο άξονας y είναι ίσος με 0.
Ρωτήθηκε επίσης, πώς βρίσκετε τις ρίζες μιας συνάρτησης σε ένα γράφημα;
ΕΝΑ ρίζα είναι μια τιμή για την οποία ένα δεδομένο λειτουργία ισούται με μηδέν. Όταν αυτό λειτουργία σχεδιάζεται σε α γραφική παράσταση , ο ρίζες είναι σημεία όπου η λειτουργία διασχίζει τον άξονα x. Για ένα λειτουργία , f(x), το ρίζες είναι οι τιμές του x για τις οποίες f(x)=0 f (x) = 0.
Επιπλέον, ποιο είναι το άθροισμα των ριζών της εξίσωσης; Αυτά ονομάζονται τα ρίζες του τετραγωνικού εξίσωση . Για ένα τετραγωνικό εξίσωση τσεκούρι2+bx+c = 0, το άθροισμα του ρίζες = –b/a και το γινόμενο του ρίζες = γ/α. Ένα τετραγωνικό εξίσωση μπορεί να εκφραστεί ως γινόμενο δύο διωνύμων.
Από αυτό, πόσες ρίζες έχει μια εξίσωση;
Αυτό σημαίνει ότι το x=0 είναι ένα από τα ρίζες . Ο βαθμός είναι 3, οπότε αναμένουμε 3 ρίζες . Υπάρχει μόνο ένας πιθανός συνδυασμός: 3 ρίζες : 1 θετικό, 0 αρνητικό και 2 σύνθετο.
Πώς λύνεις πολυωνυμικές εκφράσεις;
Βήματα
- Προσδιορίστε αν έχετε γραμμικό πολυώνυμο. Ένα γραμμικό πολυώνυμο είναι ένα πολυώνυμο πρώτου βαθμού.
- Ορίστε την εξίσωση ίση με το μηδέν. Αυτό είναι ένα απαραίτητο βήμα για την επίλυση όλων των πολυωνύμων.
- Απομονώστε τον όρο της μεταβλητής. Για να γίνει αυτό, προσθέστε ή αφαιρέστε τη σταθερά και από τις δύο πλευρές της εξίσωσης.
- Λύση για τη μεταβλητή.
Συνιστάται:
Πώς βρίσκετε τις φανταστικές ρίζες χρησιμοποιώντας τον κανόνα των ζωδίων Descartes;
Ο κανόνας των προσώπων του Ντεκάρτ λέει ότι ο αριθμός των θετικών ριζών είναι ίσος με τις αλλαγές στο πρόσημο του f(x), ή είναι μικρότερος από αυτόν κατά έναν ζυγό αριθμό (άρα συνεχίζετε να αφαιρείτε το 2 μέχρι να πάρετε είτε 1 είτε 0). Επομένως, το προηγούμενο f(x) μπορεί να έχει 2 ή 0 θετικές ρίζες. Αρνητικές πραγματικές ρίζες
Πώς βρίσκετε την ασύμπτωτη μιας λογαριθμικής εξίσωσης;
Βασικά σημεία Όταν σχηματίζεται γραφική παράσταση, η λογαριθμική συνάρτηση είναι παρόμοια σε σχήμα με τη συνάρτηση τετραγωνικής ρίζας, αλλά με κατακόρυφη ασύμπτωτη καθώς το x προσεγγίζει το 0 από τα δεξιά. Το σημείο (1,0) βρίσκεται στη γραφική παράσταση όλων των λογαριθμικών συναρτήσεων της μορφής y=logbx y = l o g b x, όπου b είναι θετικός πραγματικός αριθμός
Πώς βρίσκετε τις παρεμβολές μιας ανισότητας;
Εναλλακτικά, μπορούμε να προσδιορίσουμε την τομή x και την τομή y της τυπικής γραμμικής ανισότητας υποκαθιστώντας το y = 0, στη συνέχεια να λύσουμε το x και να υποκαταστήσουμε το x = 0 και μετά να λύσουμε το y αντίστοιχα. Θυμηθείτε ότι το thex-intercept είναι η τιμή του x όταν y = 0 και το they-intercept είναι η τιμή του y όταν x = 0
Πώς βρίσκετε τον προσανατολισμό μιας παραμετρικής εξίσωσης;
Η κατεύθυνση της επίπεδης καμπύλης καθώς αυξάνεται η παράμετρος ονομάζεται προσανατολισμός της καμπύλης. Ο προσανατολισμός μιας επίπεδης καμπύλης μπορεί να αναπαρασταθεί με βέλη που σχεδιάζονται κατά μήκος της καμπύλης. Εξετάστε το παρακάτω γράφημα. Ορίζεται από τις παραμετρικές εξισώσεις x = cos(t), y = sin(t), 0≦t < 2Π
Πώς βρίσκετε τις μονάδες μιας σταθεράς ρυθμού;
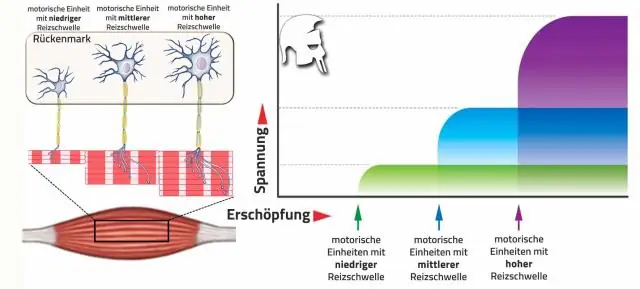
Μονάδες Για τάξη (m + n), η σταθερά ρυθμού έχει μονάδες ofmol·L·s−1 Για τάξη μηδέν, η σταθερά ρυθμού έχει μονάδες ofmol·L−1·s−1(ή M·s−1) Για την τάξη ένα , η σταθερά ρυθμού έχει μονάδες s−1 Για τη δεύτερη τάξη, η σταθερά ρυθμού έχει μονάδες L·mol−1·s−1(ή M−1·s−1)