
Πίνακας περιεχομένων:
- Συγγραφέας Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:35.
- Τελευταία τροποποίηση 2025-01-22 16:57.
Για να προσδιορίσετε την ταυτότητα διαφοράς για την εφαπτομένη, χρησιμοποιήστε το γεγονός ότι tan(−β) = −tanβ
- Παράδειγμα 1: Βρείτε την ακριβή τιμή του ηλιοκαμένος 75°.
- Παράδειγμα 2: Επιβεβαιώστε το ηλιοκαμένος (180° − x) = − ηλιοκαμένος Χ.
- Παράδειγμα 3: Επιβεβαιώστε το ηλιοκαμένος (180° + x) = ηλιοκαμένος Χ.
- Παράδειγμα 4: Επιβεβαιώστε ότι ηλιοκαμένος (360° − x) = − ηλιοκαμένος Χ.
- Παράδειγμα 5: Επαληθεύστε το Ταυτότητα .
Εξάλλου, ποιος είναι ο τύπος για την εφαπτομένη;
Σε οποιοδήποτε ορθογώνιο τρίγωνο, το εφαπτομένος μιας γωνίας είναι το μήκος της απέναντι πλευράς (Ο) διαιρούμενο με το μήκος της διπλανής πλευράς (Α). Σε ένα τύπος , γράφεται απλά ως 'tan'. Συχνά απομνημονεύεται ως "SOH" - που σημαίνει ότι το Sine είναι αντίθετο έναντι της υποτείνουσας.
Επιπλέον, πώς μπορείτε να ξαναγράψετε μια εφαπτομένη; Για να ξαναγράψετε τη συνάρτηση ημιτονοειδούς ως εφαπτομένη, ακολουθήστε τα εξής βήματα:
- Ξεκινήστε με την ταυτότητα αναλογίας που περιλαμβάνει ημίτονο, συνημίτονο και εφαπτομένη και πολλαπλασιάστε κάθε πλευρά με συνημίτονο για να λάβετε το ημίτονο μόνο στα αριστερά.
- Αντικαταστήστε το συνημίτονο με την αντίστροφη συνάρτησή του.
- Λύστε το μαύρισμα της Πυθαγόρειας ταυτότητας2θ + 1 = δευτ2θ για τομή.
Από αυτή την άποψη, ποιος είναι ο τύπος της διπλής γωνίας;
Σχετικά με το Transcript. Το συνημίτονο τύπος διπλής γωνίας μας λέει ότι το cos(2θ) είναι πάντα ίσο με το cos²θ-sin²θ. Για παράδειγμα, το cos(60) είναι ίσο με το cos²(30)-sin²(30). Μπορούμε να χρησιμοποιήσουμε αυτήν την ταυτότητα για να ξαναγράψουμε εκφράσεις ή να λύσουμε προβλήματα.
Ποια είναι η εφαπτομένη ταυτότητα;
Το άθροισμα Ταυτότητα Για εφαπτομένος παράγεται ως εξής: Για τον προσδιορισμό της διαφοράς Ταυτότητα Για εφαπτομένος , χρησιμοποιήστε το γεγονός ότι ηλιοκαμένος (−β) = −τανβ. Η διπλή γωνία Ταυτότητα Για εφαπτομένος προκύπτει χρησιμοποιώντας το άθροισμα Ταυτότητα Για εφαπτομένος . Η μισή γωνία Ταυτότητα Για εφαπτομένος μπορεί να γραφτεί σε τρεις διαφορετικές μορφές.
Συνιστάται:
Πώς λύνετε μια τετραγωνική εξίσωση χρησιμοποιώντας τον νόμο μηδενικών παραγόντων;

Από αυτό μπορούμε να συμπεράνουμε ότι: Αν το γινόμενο οποιωνδήποτε δύο αριθμών είναι μηδέν, τότε ο ένας ή και οι δύο αριθμοί είναι μηδέν. Δηλαδή, αν ab = 0, τότε a = 0 ή b = 0 (που περιλαμβάνει την πιθανότητα ότι a = b = 0). Αυτό ονομάζεται νόμος μηδενικού παράγοντα. και το χρησιμοποιούμε συχνά για να λύσουμε δευτεροβάθμιες εξισώσεις
Τι είναι οι πολυωνυμικές ταυτότητες;

Οι πολυωνυμικές ταυτότητες είναι εξισώσεις που ισχύουν για όλες τις πιθανές τιμές της μεταβλητής. Για παράδειγμα, το x²+2x+1=(x+1)² είναι μια ταυτότητα. Αυτό το εισαγωγικό βίντεο δίνει περισσότερα παραδείγματα ταυτοτήτων και συζητά πώς αποδεικνύουμε ότι μια εξίσωση είναι ταυτότητα
Ποιο οργανίδιο λειτουργεί ως το ταχυδρομείο του κυττάρου που ταξινομεί τις πρωτεΐνες και τις στέλνει στον προορισμό τους εντός ή εκτός του κυττάρου;
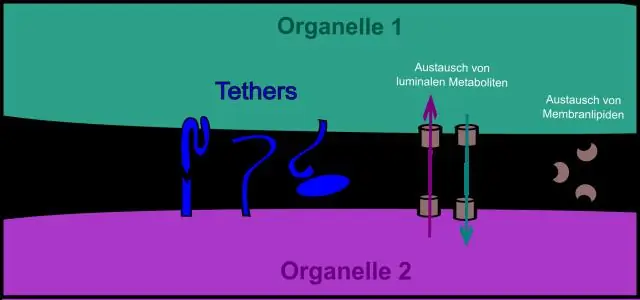
Golgi Σε σχέση με αυτό, ποιο οργανίδιο είναι υπεύθυνο για τη μεταφορά; ενδοπλασματικό δίκτυο (ER Δεύτερον, πώς κινούνται οι πρωτεΐνες μέσα στο κύτταρο; ο οι πρωτεΐνες περνούν το σύστημα της ενδομεμβράνης και αποστέλλονται από την trans όψη της συσκευής Golgi σε κυστίδια μεταφοράς που περάστε το κυτταρόπλασμα και στη συνέχεια συντήκονται με την πλασματική μεμβράνη απελευθερώνοντας το πρωτεΐνη προς το εξωτερικό του κύτταρο .
Πώς λύνετε τις ποσοστιαίες αναλογίες;
Σε μια αναλογία τα διασταυρούμενα προϊόντα είναι ίσα: Άρα 3 φορές το 100 είναι ίσο με 4 φορές το ΠΟΣΟΣΤΟ. Το PERCENT που λείπει ισούται με 100 επί το 3 διαιρούμενο με το 4. (Πολλαπλασιάστε τις δύο απέναντι γωνίες με αριθμούς και μετά διαιρέστε με τον άλλο αριθμό.)
Πώς οι άνθρωποι άλλαξαν για πρώτη φορά τις καλλιέργειες Ποια μέθοδο χρησιμοποιούν οι επιστήμονες σήμερα για να αλλάξουν τις καλλιέργειες;

Από τα αγγούρια και τα καρότα μέχρι το λευκό ρύζι και το σιτάρι, εμείς οι άνθρωποι έχουμε αλλάξει τα γονίδια σχεδόν κάθε τροφής που τρώμε. Σήμερα οι επιστήμονες μπορούν να παράγουν γρήγορα μια αλλαγή επιλέγοντας ένα μόνο γονίδιο που μπορεί να οδηγήσει σε ένα επιθυμητό χαρακτηριστικό και εισάγοντας αυτό το γονίδιο απευθείας στο χρωμόσωμα ενός οργανισμού
