Βίντεο: Τι είναι οι πολυωνυμικές ταυτότητες;
2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35
Πολυωνυμικές ταυτότητες είναι εξισώσεις που ισχύουν για όλες τις πιθανές τιμές της μεταβλητής. Για παράδειγμα, το x²+2x+1=(x+1)² είναι an Ταυτότητα . Αυτό το εισαγωγικό βίντεο παρέχει περισσότερα παραδείγματα ταυτότητες και συζητά πώς αποδεικνύουμε ότι μια εξίσωση είναι α Ταυτότητα.
Από αυτό, ποιες είναι οι έγκυρες ταυτότητες;
Αν μια εξίσωση περιέχει μία ή περισσότερες μεταβλητές και είναι έγκυρος για όλες τις τιμές αντικατάστασης των μεταβλητών για τις οποίες ορίζονται και οι δύο πλευρές της εξίσωσης, τότε η εξίσωση είναι γνωστή ως Ταυτότητα . Η εξίσωση x 2 + 2 x = x(x + 2), για παράδειγμα, είναι an Ταυτότητα επειδή είναι έγκυρος για όλες τις τιμές αντικατάστασης του x.
Στη συνέχεια, το ερώτημα είναι τι είναι ο πολυωνυμικός τύπος; Τύπος πολυωνυμικών εξισώσεων Συνήθως, το πολυωνυμική εξίσωση εκφράζεται με τη μορφή α (Χ). Παράδειγμα α πολυωνυμική εξίσωση είναι: 2x2 + 3x + 1 = 0, όπου 2x2 Το + 3x + 1 είναι βασικά α πολυώνυμος έκφραση που έχει οριστεί ίση με το μηδέν, για να σχηματίσει α πολυωνυμική εξίσωση.
Επιπλέον, ποιες είναι οι αλγεβρικές ταυτότητες;
Ενα αλγεβρική ταυτότητα είναι μια ισότητα που ισχύει για οποιεσδήποτε τιμές των μεταβλητών του. Για παράδειγμα, το Ταυτότητα (x + y) 2 = x 2 + 2 xy + y 2 (x+y)^2 = x^2 + 2xy + y^2 (x+y)2=x2+2xy+y2 ισχύει για όλες τις τιμές του x και y.
Πώς επαληθεύετε την αλγεβρική ταυτότητα;
Αλγεβρική ταυτότητα (α+β)2 = α2 + 2αβ + β2 επαληθεύεται. ο Ταυτότητα (α+β)2 = α2 + 2αβ + β2 επαληθεύεται με κοπή και επικόλληση χαρτιού. Αυτό Ταυτότητα μπορεί να επαληθευτεί γεωμετρικά λαμβάνοντας άλλες τιμές των a και b.
Συνιστάται:
Τι είναι η κοινωνιοβιολογία και ποιες είναι οι κύριες επικρίσεις σε αυτήν;
Μια σχετική πτυχή της κοινωνιοβιολογίας ασχολείται με τις αλτρουιστικές συμπεριφορές γενικά. Οι επικριτές κατηγόρησαν ότι αυτή η εφαρμογή της κοινωνιοβιολογίας ήταν μια μορφή γενετικού ντετερμινισμού και ότι δεν έλαβε υπόψη την πολυπλοκότητα της ανθρώπινης συμπεριφοράς και τον αντίκτυπο του περιβάλλοντος στην ανθρώπινη ανάπτυξη
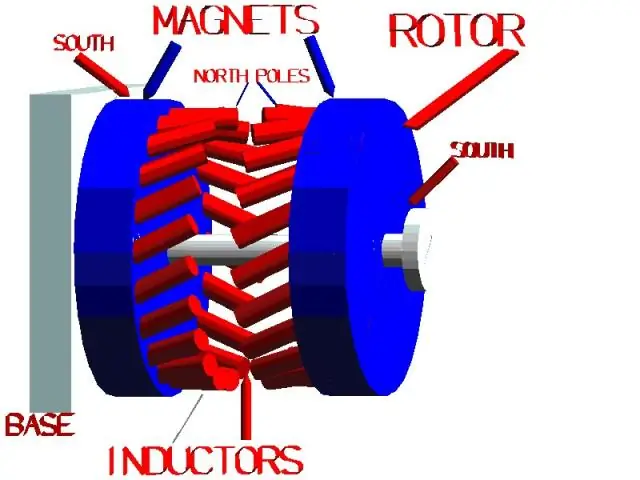
Γιατί το επαγόμενο emf είναι μηδέν όταν η μαγνητική ροή είναι μέγιστη;
Όταν το πηνίο είναι όρθιο, δεν υπάρχει αλλαγή στη μαγνητική ροή (δηλαδή emf=0) επειδή το πηνίο δεν «κόβει» τις γραμμές πεδίου. Το επαγόμενο emf είναι μηδέν όταν τα πηνία είναι κάθετα στις γραμμές πεδίου και μέγιστο όταν είναι παράλληλες. Θυμηθείτε, το επαγόμενο emf είναι ο ρυθμός αλλαγής στη σύνδεση μαγνητικής ροής
Είναι η ενέργεια που ταξιδεύει με ακτινοβολία Ένα παράδειγμα αυτού είναι το φως;
2) Το φως ταξινομείται ως ηλεκτρομαγνητική ακτινοβολία επειδή τα ηλεκτρικά και μαγνητικά πεδία δονούνται σε ένα φωτεινό κύμα. ΡΑΔΙΑΝΤΙΚΗ ΕΝΕΡΓΕΙΑ - είναι ενέργεια που ταξιδεύει με ακτινοβολία. Ένα παράδειγμα αυτού είναι το φως. 4) Η θερμική ακτινοβολία, γνωστή και ως _ΥΠΕΡΥΘΡΑ ΚΥΜΑΤΑ που δεν μπορούν να φανούν από τα μάτια σας αλλά μπορούν να γίνουν αισθητές από το δέρμα σας
Πώς λύνετε τις ταυτότητες Ταν;
Για να προσδιορίσετε την ταυτότητα διαφοράς για την εφαπτομένη, χρησιμοποιήστε το γεγονός ότι tan(−β) = −tanβ. Παράδειγμα 1: Βρείτε την ακριβή τιμή του μαυρίσματος 75°. Παράδειγμα 2: Επαληθεύστε ότι το tan (180° − x) = −tan x. Παράδειγμα 3: Επαληθεύστε ότι tan (180° + x) = tan x. Παράδειγμα 4: Επαληθεύστε ότι το tan (360° − x) = − tan x. Παράδειγμα 5: Επαληθεύστε την ταυτότητα
Τι είναι ένα απολίθωμα δείκτη Ποιες είναι οι δύο προϋποθέσεις για να είναι ένα απολίθωμα δείκτη;
Ένα χρήσιμο απολίθωμα δείκτη πρέπει να είναι διακριτικό ή εύκολα αναγνωρίσιμο, άφθονο και να έχει ευρεία γεωγραφική κατανομή και μικρή χρονική εμβέλεια. Τα απολιθώματα δεικτών αποτελούν τη βάση για τον καθορισμό των ορίων στη γεωλογική χρονική κλίμακα και για τη συσχέτιση των στρωμάτων