Πίνακας περιεχομένων:
Βίντεο: Πώς λύνεις τον συντελεστή συμπληρώνοντας το τετράγωνο;
2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35
Τώρα μπορούμε να λύσουμε μια Τετραγωνική Εξίσωση σε 5 βήματα:
- Βήμα 1 Διαιρέστε όλους τους όρους με ένα (το συντελεστής του x2).
- Βήμα 2 Μετακινήστε τον αριθμητικό όρο (c/a) στη δεξιά πλευρά της εξίσωσης.
- Βήμα 3 Συμπληρώστε το τετράγωνο στην αριστερή πλευρά της εξίσωσης και ισορροπήστε αυτό προσθέτοντας την ίδια τιμή στη δεξιά πλευρά της εξίσωσης.
Με αυτόν τον τρόπο, τι είναι οι συντελεστές;
Στα μαθηματικά, α συντελεστής είναι ένας πολλαπλασιαστικός παράγοντας σε κάποιο όρο ενός πολυωνύμου, μιας σειράς ή οποιασδήποτε έκφρασης. είναι συνήθως ένας αριθμός, αλλά μπορεί να είναι οποιαδήποτε έκφραση. Για παράδειγμα, εάν το y θεωρείται ως παράμετρος στην παραπάνω παράσταση, το συντελεστής του x είναι −3y και η σταθερά συντελεστής είναι 1,5 + y.
Δεύτερον, πότε δεν μπορείς να συμπληρώσεις το τετράγωνο; Με την ευκαιρία, εκτός αν εσείς το λένε εσείς πρέπει να χρησιμοποιήσετε ολοκληρώνοντας την πλατεία , εσύ θα Πιθανώς να μην χρησιμοποιήσει ποτέ αυτή τη μέθοδο στην πραγματική πράξη κατά την επίλυση δευτεροβάθμιων εξισώσεων. Είτε κάποια άλλη μέθοδο (όπως η παραγοντοποίηση) θα να είναι προφανής και πιο γρήγορη, διαφορετικά η Τετραγωνική Φόρμουλα (ανασκόπηση στη συνέχεια) θα να είναι πιο εύκολο στη χρήση.
Συνεπώς, ποια σταθερά πρέπει να προστεθεί για να συμπληρωθεί το τετράγωνο;
ο συνεχής οι οποίες πρέπει να προστεθεί και αφαιρείται το (Β) 1/64. χρησιμοποιείται για την επίλυση της δευτεροβάθμιας εξίσωσης με το ολοκληρώνοντας το τετράγωνο.
Πότε πρέπει να συμπληρώσω το τετράγωνο;
Στη συνέχεια, αν ο συντελεστής του τετραγώνου είναι 1 και ο συντελεστής του γραμμικού (μεσαίου) μέλους είναι άρτιος, ολοκληρώνοντας την πλατεία είναι μια καλή μέθοδος προς το χρήση. Τέλος, ο τετραγωνικός τύπος θα λειτουργήσει σε οποιαδήποτε τετραγωνική εξίσωση.
Συνιστάται:
Πώς βρίσκετε τον συντελεστή κλίμακας μιας διαστολής σε ένα επίπεδο συντεταγμένων;
Γράφημα το τρίγωνο ABC με τις συντεταγμένες A(2, 6), B(2, 2), C(6, 2). Στη συνέχεια διαστέλλετε την εικόνα κατά συντελεστή κλίμακας 1/2 με την αρχή ως κέντρο διαστολής. Αρχικά, γράφουμε το αρχικό μας τρίγωνο στο επίπεδο συντεταγμένων. Στη συνέχεια, πολλαπλασιάζουμε κάθε συντεταγμένη με τον παράγοντα κλίμακας 1/2
Είναι το τετράγωνο της αμαρτίας x ίσο με το τετράγωνο της αμαρτίας x;
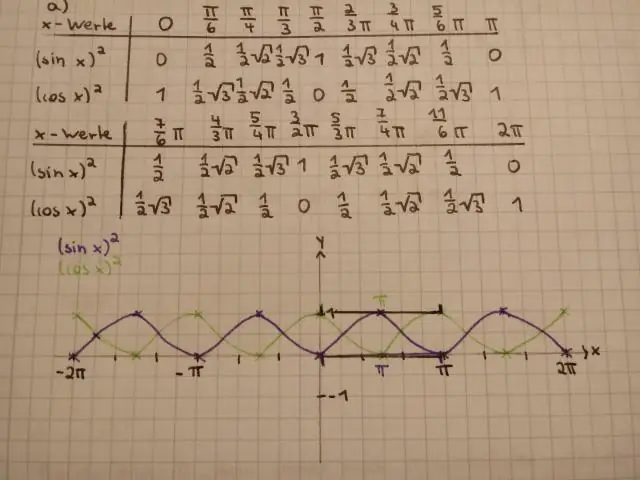
Ναι είναι. sin^2x είναι το ίδιο assinx^2 γιατί και στις δύο περιπτώσεις το '^2' σχετίζεται μόνο με το x
Πώς υπολογίζετε τον συντελεστή κατανομής;
Ο συντελεστής κατανομής είναι ο λόγος της συγκέντρωσης μιας ουσίας σε ένα μέσο ή φάση (C1) προς τη συγκέντρωση σε μια δεύτερη φάση (C2) όταν οι δύο συγκεντρώσεις βρίσκονται σε ισορροπία. δηλαδή συντελεστής κατανομής = (C1/C2)ισ. Οι μονάδες των C1 και C2 μπορεί να είναι διαφορετικές
Πώς βρίσκετε τον συντελεστή συχνότητας στην ενέργεια ενεργοποίησης;
Η εξίσωση Arrhenius είναι k = Ae^(-Ea/RT), όπου A είναι η συχνότητα ή ο προεκθετικός παράγοντας ande^(-Ea/RT) είναι το κλάσμα των συγκρούσεων που έχουν αρκετή ενέργεια για να αντιδράσουν (δηλαδή έχουν ενέργεια μεγαλύτερη από ίση στην ενέργεια ενεργοποίησης Ea) σε θερμοκρασίαT
Πώς βρίσκετε τον κύριο συντελεστή και την τελική συμπεριφορά;
Εάν η μεταβλητή (ας πούμε Χ) είναι αρνητική, τότε το Χ στον όρο υψηλότερου βαθμού δημιουργεί αρνητικό. Στη συνέχεια πολλαπλασιάζουμε τον συντελεστή του κύριου όρου με ένα αρνητικό για να προσδιορίσουμε την τελική συμπεριφορά