
Πίνακας περιεχομένων:
- Συγγραφέας Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:35.
- Τελευταία τροποποίηση 2025-01-22 16:57.
Σχεδίασε ένα τετράγωνο χωρισμένο σε τέσσερα μέρη. Βάλτε κάθε γονότυπο του γονέα πάνω από κάθε μικρό κουτί στην κορυφή του μεγάλου τετράγωνο , και των άλλων γονέων στην αριστερή πλευρά (πάνω προς τα κάτω) δίπλα σε κάθε μικρό κουτί. Το υπολειπόμενο αλληλόμορφο, ή το πεζό γράμμα, έρχεται μετά το κεφαλαίο.
Κατά συνέπεια, πώς λειτουργούν τα τετράγωνα Punnett;
ο Punnett Το τετράγωνο είναι ένα τετράγωνο διάγραμμα που χρησιμοποιείται για την πρόβλεψη των γονότυπων ενός συγκεκριμένου πειράματος διασταύρωσης ή αναπαραγωγής. Πήρε το όνομά του από τον Reginald C. Punnett , ο οποίος επινόησε την προσέγγιση. Το διάγραμμα χρησιμοποιείται από τους βιολόγους για να προσδιορίσουν την πιθανότητα ένας απόγονος να έχει συγκεκριμένο γονότυπο.
Εκτός από το παραπάνω, πώς μπορώ να φτιάξω ένα Punnett Square στο Word; Υπάρχουν τα παρακάτω βήματα με τα οποία μπορούμε σχεδιάστε ένα τετράγωνο Punnett εύκολα στην ΠΣ Λέξη : Βήμα 1: Σχεδιάζω ένα τετράγωνο από 2 * 2, Καταγράψτε όλα τα συμμετέχοντα αλληλόμορφα. Βήμα 2: Ελέγξτε τους γονότυπους για τους γονείς. Βήμα 3: Επισημάνετε τις σειρές του με τον γονότυπο ενός γονέα και μετά, προσθέστε ετικέτα στις στήλες.
Στη συνέχεια, κάποιος μπορεί επίσης να ρωτήσει, πώς μπορείτε να κάνετε τετράγωνα Punnett με δύο χαρακτηριστικά;
Είναι σημαντικό να ακολουθήσετε τα απαραίτητα βήματα
- Πρώτα πρέπει να δημιουργήσετε τον γονικό σας σταυρό, ή P1.
- Στη συνέχεια, πρέπει να φτιάξετε ένα τετράγωνο Punnett τετράγωνο 16 για τα 2 χαρακτηριστικά σας που θέλετε να διασχίσετε.
- Το επόμενο βήμα είναι να προσδιοριστούν οι γονότυποι των δύο γονέων και να τους αντιστοιχιστούν γράμματα για να αναπαραστήσουν τα αλληλόμορφα.
Πόσο ακριβή είναι τα Punnett Squares;
Είναι τέλεια ακριβής , όσο πάει. Δηλαδή, περιγράφει σωστά τη στατιστική σχέση μεταξύ των αλληλόμορφων και των Μεντελιανών φαινοτύπων. Ωστόσο, όπως σε όλη την επιστήμη, ο πραγματικός κόσμος είναι πιο περίπλοκος από τη θεωρία.
Συνιστάται:
Πώς φτιάχνεις ένα τετράγωνο Punnett;
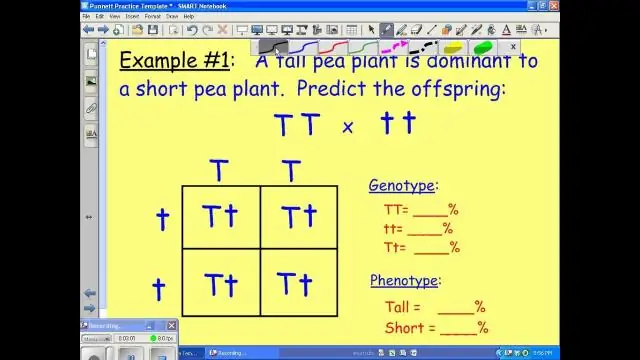
Βήματα Σχεδιάστε ένα τετράγωνο 2 x 2. Ονομάστε τα αλληλόμορφα που εμπλέκονται. Ελέγξτε τους γονότυπους των γονέων. Επισημάνετε τις σειρές με τον γονότυπο του ενός γονέα. Επισημάνετε τις στήλες με τον γονότυπο του άλλου γονέα. Ζητήστε από κάθε πλαίσιο να κληρονομήσει γράμματα από τη σειρά και τη στήλη του. Ερμηνεύστε την πλατεία Punnett. Περιγράψτε τον φαινότυπο
Ποια είναι η γενιά f1 σε ένα τετράγωνο Punnett;

Αντιπροσωπεύεται από το γράμμα N (που σημαίνει ότι είναι απλοειδή - περιέχουν τα μισά χρωμοσώματα; Γενιά P: Η γονική γενιά (συνήθως η πρώτη σε μια γενετική διασταύρωση) ; Γενιά F1: Η πρώτη γενιά απογόνων από τη γενιά P (σημαίνει πρώτο υιικό: Λατινικά για 'γιος') Γενιά F2: Η δεύτερη γενιά απογόνων
Πώς μπορείτε να κάνετε ένα τετράγωνο Punnett με πολλαπλά αλληλόμορφα;
Είναι σημαντικό να ακολουθήσετε τα απαραίτητα βήματα! Πρώτα πρέπει να δημιουργήσετε τον γονικό σας σταυρό, ή P1. Στη συνέχεια, πρέπει να φτιάξετε ένα τετράγωνο Punnett τετράγωνο 16 για τα 2 χαρακτηριστικά σας που θέλετε να διασχίσετε. Το επόμενο βήμα είναι να προσδιοριστούν οι γονότυποι των δύο γονέων και να τους αντιστοιχιστούν γράμματα για να αναπαραστήσουν τα αλληλόμορφα
Είναι το τετράγωνο της αμαρτίας x ίσο με το τετράγωνο της αμαρτίας x;
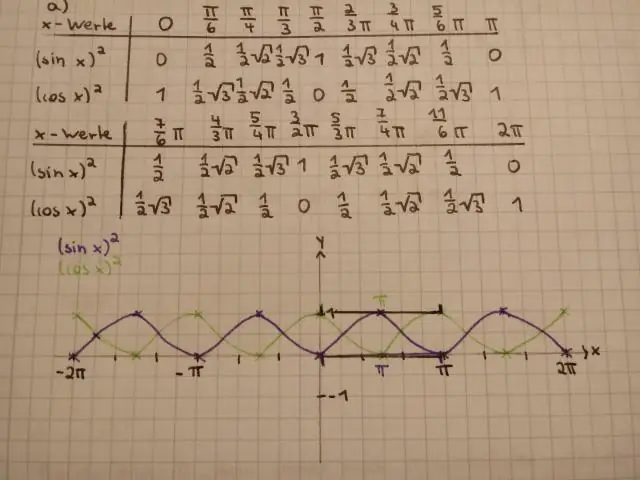
Ναι είναι. sin^2x είναι το ίδιο assinx^2 γιατί και στις δύο περιπτώσεις το '^2' σχετίζεται μόνο με το x
Τι ονομάζεται τετράγωνο τετράγωνο;

Tesseract: Ένας 4D κύβος Με απλά λόγια, ένα tesseract είναι ένας κύβος σε 4-διάστατο χώρο
