Ποια είναι τα μέτρα κεντρικής τάσης για μη ομαδοποιημένα δεδομένα;

Πίνακας περιεχομένων:

Περίληψη

Βίντεο: Ποια είναι τα μέτρα κεντρικής τάσης για μη ομαδοποιημένα δεδομένα;

2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35

Ο όρος κεντρική τάση αναφέρεται στη μέση, ή τυπική, τιμή ενός συνόλου δεδομένα , που είναι πιο συνηθισμένο μετρημένος χρησιμοποιώντας τα τρία m: μέσος όρος, διάμεσος και τρόπος λειτουργίας. Ο μέσος όρος, ο διάμεσος και ο τρόπος είναι γνωστοί ως το μέτρα κεντρικής τάσης.

Με αυτόν τον τρόπο, ποια είναι τα μέτρα κεντρικής τάσης για ομαδοποιημένα δεδομένα;

Μέση, διάμεσος, Λειτουργία: Μέτρα Κεντρικής Τάσης . MEAN Σημαίνει για Ομαδοποιημένα δεδομένα Ομαδοποιημένα δεδομένα είναι οι δεδομένα ή βαθμολογίες που είναι διατεταγμένες σε κατανομή συχνότητας.

Ομοίως, πώς λύνετε τη μέση τιμή για μη ομαδοποιημένα δεδομένα; Βήματα

Συλλέξτε και μετρήστε τα δεδομένα σας. Για οποιοδήποτε σύνολο τιμών δεδομένων, ο μέσος όρος είναι ένα μέτρο της κεντρικής τιμής.
Βρείτε το άθροισμα των τιμών των δεδομένων. Το πρώτο βήμα για την εύρεση του μέσου όρου είναι ο υπολογισμός του αθροίσματος όλων των σημείων δεδομένων.
Διαιρέστε για να βρείτε τη μέση τιμή. Τέλος, διαιρέστε το άθροισμα με τον αριθμό των τιμών.

Επιπλέον, ποιος είναι ο τύπος που χρησιμοποιείται για την εύρεση της μέσης διάμεσης τιμής και της λειτουργίας για μη ομαδοποιημένα δεδομένα;

Περίληψη

Για ομαδοποιημένα δεδομένα, δεν μπορούμε να βρούμε την ακριβή Μέση, Μέση και Κατάσταση, μπορούμε μόνο να δώσουμε εκτιμήσεις.
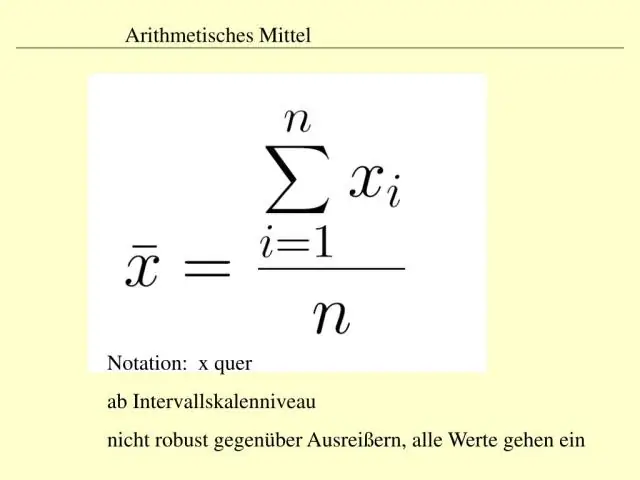
Για να υπολογίσετε τη Μέση τιμή, χρησιμοποιήστε τα μέσα των διαστημάτων κλάσης: Εκτιμώμενος μέσος όρος = Άθροισμα (Μεσαίο σημείο × Συχνότητα) Άθροισμα συχνότητας.
Για την εκτίμηση της διάμεσης χρήσης: Εκτιμώμενη διάμεσος = L + (n/2) − BG × w.
Για να εκτιμήσετε τη λειτουργία, χρησιμοποιήστε:

Ποιος είναι ο τύπος λειτουργίας για ομαδοποιημένα δεδομένα;

Η δασκάλα μας λέει στον α τύπος να μάθω τρόπος , δηλαδή Z=L1+(F1-F0)/(2F1-F0-F2)*i όπου: L1 = κατώτερο όριο της κλάσης τρόπων F1 = συχνότητα τροπικής κατηγορίας. F2 = αμέσως μετά τη συχνότητα κλάσης τρόπων. F0 = μόλις προηγηθεί η συχνότητα της τροπικής κλάσης.

Συνιστάται:

Ποια είναι η διαφορά μεταξύ της τάσης γραμμής σε γραμμή και τάσης γραμμής σε ουδέτερο;

Η τάση μεταξύ δύο γραμμών (για παράδειγμα «L1» και «L2») ονομάζεται τάση γραμμής προς γραμμή (ή φάσης προς φάση). Η τάση σε κάθε τύλιγμα (για παράδειγμα μεταξύ 'L1' και 'N' ονομάζεται γραμμή προς ουδέτερο (ή τάση φάσης)

Ποια είναι τα μέτρα γωνίας που λείπουν στο τρίγωνο ABC;

Εξήγηση βήμα προς βήμα: Δίνεται ότι το ABC είναι ένα ορθογώνιο τρίγωνο το οποίο είναι ορθογώνιο σε C και AC=7 ίντσες και CB=5 ίντσες. Επομένως, το μέτρο των γωνιών που λείπουν στο τρίγωνο ABC είναι 35,5° και 54,5° αντίστοιχα

Τι είναι τα μη ομαδοποιημένα δεδομένα στις στατιστικές;

Τα μη ομαδοποιημένα δεδομένα είναι τα δεδομένα που συλλέγετε αρχικά από ένα πείραμα ή μελέτη. Τα δεδομένα είναι ακατέργαστα - δηλαδή, δεν ταξινομούνται σε κατηγορίες, ταξινομούνται ή ομαδοποιούνται με άλλο τρόπο. Ένα μη ομαδοποιημένο σύνολο δεδομένων είναι βασικά μια λίστα αριθμών

Ποια είναι τα μέτρα της ένωσης;

Ένα μέτρο συσχέτισης ποσοτικοποιεί τη σχέση μεταξύ έκθεσης και ασθένειας μεταξύ των δύο ομάδων. Παραδείγματα μετρήσεων συσχέτισης περιλαμβάνουν αναλογία κινδύνου (σχετικός κίνδυνος), αναλογία ποσοστού, αναλογία πιθανοτήτων και αναλογικό λόγο θνησιμότητας