- Συγγραφέας Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:35.
- Τελευταία τροποποίηση 2025-01-22 16:57.
Ένα από τα πλεονεκτήματα του παραμετρικές εξισώσεις είναι ότι μπορούν να είναι μεταχειρισμένος για να σχηματίσετε καμπύλες που δεν είναι συναρτήσεις, όπως ο μοναδιαίος κύκλος. Ένα άλλο πλεονέκτημα του παραμετρικές εξισώσεις είναι ότι η παράμετρος μπορεί να είναι μεταχειρισμένος για να αναπαραστήσουν κάτι χρήσιμο και επομένως να μας δώσουν πρόσθετες πληροφορίες για το γράφημα.
Γνωρίζετε επίσης, σε τι χρησιμεύουν οι παραμετρικές εξισώσεις;
Παραμετρικές εξισώσεις είναι συνήθως συνηθισμένος εκφράστε τις συντεταγμένες των σημείων που συνθέτουν ένα γεωμετρικό αντικείμενο όπως μια καμπύλη ή μια επιφάνεια, οπότε το εξισώσεις ονομάζονται συλλογικά α παραμετρική αναπαράσταση ή παραμετροποίηση (εναλλακτικά γραφή ως παραμετροποίηση) του αντικειμένου.
Εκτός από τα παραπάνω, πώς λειτουργούν οι παραμετρικές εξισώσεις; Παραμετρικές εξισώσεις χρησιμοποιούνται όταν το x και το y δεν σχετίζονται άμεσα μεταξύ τους, αλλά συνδέονται και τα δύο μέσω ενός τρίτου όρου. Στο παράδειγμα, η θέση του αυτοκινήτου στην κατεύθυνση x αλλάζει γραμμικά με το χρόνο, δηλαδή το γράφημα της συνάρτησής του είναι μια ευθεία γραμμή.
Επιπλέον, τι σημαίνει παραμετρική συνάρτηση;
Παραμετρικές συναρτήσεις : Ορισμός Παραμετρικές συναρτήσεις είναι λειτουργίες ενός αριθμού συντεταγμένων (2 για το δισδιάστατο επίπεδο, 3 για τον τρισδιάστατο χώρο και ούτω καθεξής), όπου καθεμία από τις συντεταγμένες (x, y, z) εκφράζεται ως άλλη λειτουργία κάποιας παραμέτρου, όπως ο χρόνος: x = f(t), y = g(t), z = h(t) και ούτω καθεξής.
Ποιος ανακάλυψε τις παραμετρικές εξισώσεις;
Ο όρος παραμετρική προέρχεται από τα μαθηματικά, αλλά υπάρχει συζήτηση για το πότε οι σχεδιαστές άρχισαν αρχικά να χρησιμοποιούν τη λέξη. David Gerber (2007, 73), στη διδακτορική του διατριβή Παραμετρική Πρακτική, πιστώνει στον Maurice Ruiter για την πρώτη χρήση του όρου σε μια εργασία από το 1988 με τίτλο Παραμετρική Σχεδιασμός [1].
Συνιστάται:
Γιατί χρησιμοποιούνται διανύσματα στη μηχανική μάθηση;

Στη μηχανική μάθηση, τα διανύσματα χαρακτηριστικών χρησιμοποιούνται για να αναπαραστήσουν αριθμητικά ή συμβολικά χαρακτηριστικά, που ονομάζονται χαρακτηριστικά, ενός αντικειμένου με μαθηματικό, εύκολα αναλύσιμο τρόπο. Είναι σημαντικά για πολλούς διαφορετικούς τομείς της μηχανικής μάθησης και της επεξεργασίας προτύπων
Γιατί προσαρμόζουμε τους συντελεστές όταν εξισορροπούμε χημικές εξισώσεις και όχι δείκτες;

Όταν αλλάζετε τους συντελεστές, αλλάζετε μόνο τον αριθμό των μορίων της συγκεκριμένης ουσίας. Ωστόσο, όταν αλλάζετε τους δείκτες, αλλάζετε την ίδια την ουσία, κάτι που θα κάνει τη χημική σας εξίσωση λανθασμένη
Γιατί χρησιμοποιούνται κυρτές καθρέφτες στα σούπερ μάρκετ;

Ο κυρτός καθρέφτης χρησιμοποιείται στα σούπερ μάρκετ γιατί καλύπτει μια μεγάλη περιοχή στις κάμερες cc και κάνει τα λαχανικά και τα φρούτα να φαίνονται σωστά
Πώς χρησιμοποιούνται οι κυριολεκτικές εξισώσεις στην πραγματική ζωή;
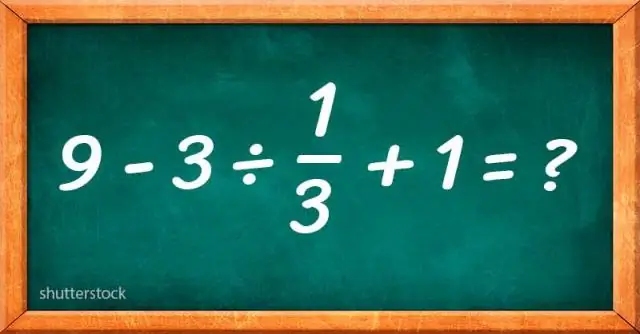
Η επίλυση κυριολεκτικών εξισώσεων είναι συχνά χρήσιμη σε πραγματικές καταστάσεις, για παράδειγμα μπορούμε να λύσουμε τον τύπο για την απόσταση, d = rt, για r για να παράγουμε μια εξίσωση για το ρυθμό. Θα χρειαστούμε όλες τις μεθόδους από την επίλυση εξισώσεων πολλαπλών βημάτων. Επίλυση μιας μεταβλητής σε έναν τύπο
Ποια είναι μερικά παραδείγματα όπου χρησιμοποιούνται οι εξισώσεις κίνησης;

Εξισώσεις κίνησης για ομοιόμορφη επιτάχυνση Το τζόκινγκ, η οδήγηση αυτοκινήτου, ακόμη και η απλή βόλτα είναι όλα καθημερινά παραδείγματα κίνησης. Οι σχέσεις μεταξύ αυτών των μεγεθών είναι γνωστές ως εξισώσεις κίνησης
