Πίνακας περιεχομένων:
Βίντεο: Πώς χρησιμοποιείτε συμβατούς αριθμούς για την εκτίμηση της διαίρεσης;
2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2024-01-18 08:14
Περίληψη
- Συμβατοί αριθμοί είναι αριθμοί που βρίσκονται κοντά στο αριθμοί το αντικαθιστούν διαιρέστε ομοιόμορφα μεταξύ τους.
- Το πηλίκο είναι το αποτέλεσμα που παίρνετε όταν το κάνετε διαιρέστε .
- Το 56.000 είναι πολύ κοντά στο 55.304.
- Το 800 είναι πολύ κοντά στο 875, ΚΑΙ διαιρείται ομοιόμορφα σε 56.000.
Ομοίως, πώς χρησιμοποιείτε συμβατούς αριθμούς για την εκτίμηση;
- Οι συμβατοί αριθμοί είναι ζεύγη αριθμών που είναι εύκολο να προστεθούν, να αφαιρεθούν, να πολλαπλασιαστούν ή να διαιρεθούν διανοητικά. Όταν χρησιμοποιείτε την εκτίμηση για να προσεγγίσετε έναν υπολογισμό, αντικαταστήστε τους πραγματικούς αριθμούς με συμβατούς αριθμούς.
- Παράδειγμα 1 (Προσθήκη) 500 + 300 = 800.
- Παράδειγμα 2 (Αφαίρεση) 19,4 − 3,8 = 15,6.
- Παράδειγμα 3 (Πολλαπλασιασμός)
Επιπλέον, ποιοι είναι οι συμβατοί αριθμοί; Στα μαθηματικά, συμβατούς αριθμούς είναι οι αριθμοί που είναι εύκολο να προστεθούν, να αφαιρεθούν, να πολλαπλασιαστούν ή να διαιρεθούν διανοητικά. Συμβατοί αριθμοί είναι κοντά σε αξία με την πραγματική αριθμοί που διευκολύνουν την εκτίμηση της απάντησης και τον υπολογισμό των προβλημάτων.
Εκτός από τα παραπάνω, πώς μπορείτε να χρησιμοποιήσετε έναν συμβατό αριθμό για να υπολογίσετε ένα πηλίκο όταν διαιρείτε ένα δεκαδικό με έναν ακέραιο αριθμό;
Περίληψη: Κατά τη διαίρεση ενός δεκαδικού με έναν ακέραιο αριθμό, χρησιμοποιούμε την ακόλουθη διαδικασία:
- Υπολογίστε το πηλίκο.
- Εκτελέστε τη διαίρεση. Θυμηθείτε να τοποθετήσετε ένα μηδέν στο πηλίκο όταν ο διαιρέτης είναι μεγαλύτερος από το μέρισμα.
- Συγκρίνετε την εκτίμησή σας με το πηλίκο σας για να επαληθεύσετε ότι η απάντηση έχει νόημα.
Ποια είναι η διαφορά μεταξύ συμβατών αριθμών και στρογγυλοποίησης;
Χρησιμοποιούμε συμβατούς αριθμούς για να λύσουμε ευκολότερα το πρόβλημα στο κεφάλι μας στρογγύλεμα καθε αριθμός με ακρίβεια δέκα, είκοσι, πενήντα ή εκατό. Αν όμως φτιάξουμε το αριθμοί συμβατοί και στρογγυλοποιούμε στο πλησιέστερο εκατό ή δέκα σημείο, τα 300 και 350 είναι πολύ πιο εύκολο να υπολογιστούν στο μυαλό μας.
Συνιστάται:
Πώς υπολογίζετε την εκτίμηση διαστήματος;
Για το μέγεθος του δείγματος (n). και διαιρέστε το με την τετραγωνική ρίζα του n. Αυτός ο υπολογισμός σας δίνει το περιθώριο σφάλματος. Statistics For Dummies, 2nd Edition. Επίπεδο εμπιστοσύνης z*-τιμή 90% 1,645 (κατά σύμβαση) 95% 1,96 98% 2,33 99% 2,58
Πώς χρησιμοποιείτε τους τύπους στους Αριθμούς;
Εισαγωγή τύπου Κάντε κλικ στο κελί όπου θέλετε να εμφανίζεται το αποτέλεσμα και, στη συνέχεια, πληκτρολογήστε το σύμβολο ίσου (=). Κάντε κλικ σε ένα κελί για χρήση στον τύπο σας ή πληκτρολογήστε μια τιμή (για παράδειγμα, έναν αριθμό όπως 0 ή 5,20). Πληκτρολογήστε έναν αριθμητικό τελεστή (για παράδειγμα, +, -, * ή /), στη συνέχεια επιλέξτε ένα άλλο κελί που θα χρησιμοποιήσετε στον τύπο σας ή πληκτρολογήστε μια τιμή
Ποια είναι η διαφορά μεταξύ της διατήρησης της ενέργειας και της αρχής της διατήρησης της ενέργειας;
Η θερμιδική θεωρία υποστήριζε ότι η θερμότητα δεν μπορούσε ούτε να δημιουργηθεί ούτε να καταστραφεί, ενώ η διατήρηση της ενέργειας συνεπάγεται την αντίθετη αρχή ότι η θερμότητα και η μηχανική εργασία είναι εναλλάξιμα
Πώς χρησιμοποιείτε τους φανταστικούς αριθμούς σε μια αριθμομηχανή;
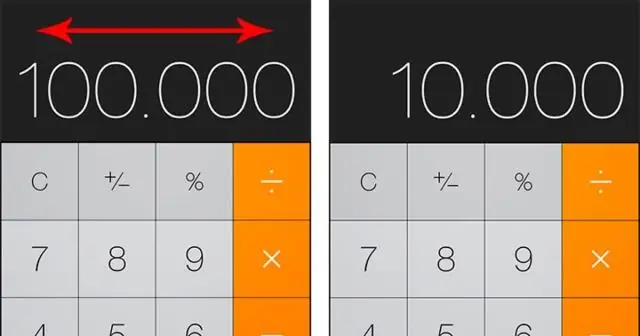
Η αριθμομηχανή σας εμφανίζει μόνο την απλοποιημένη απάντηση, όπως φαίνεται στην πρώτη οθόνη. Οι μιγαδικοί αριθμοί δεν μπορούν να χρησιμοποιηθούν με το πρότυπο κλάσματος n/d. Αντίθετα, εισαγάγετε μιγαδικούς αριθμούς ως κλάσματα χρησιμοποιώντας παρενθέσεις και το κλειδί διαίρεσης. Πατήστε [MATH][ENTER][ENTER] για να εμφανιστεί η απάντηση του μιγαδικού αριθμού σε μορφή κλασμάτων
Υπάρχει μια ιδιότητα κλεισίματος της αφαίρεσης που ισχύει για ακέραιους αριθμούς;
Το κλείσιμο είναι μια μαθηματική ιδιότητα που σχετίζεται με σύνολα αριθμών και πράξεων. Εάν η πράξη σε δύο αριθμούς στο σύνολο παράγει έναν αριθμό που βρίσκεται στο σύνολο, έχουμε κλείσιμο. Βρήκαμε ότι το σύνολο των ακέραιων αριθμών δεν είναι κλειστό με αφαίρεση, αλλά το σύνολο των ακεραίων είναι κλειστό υποαφαίρεση