Ποια είναι η εξίσωση της τετραγωνικής συνάρτησης;

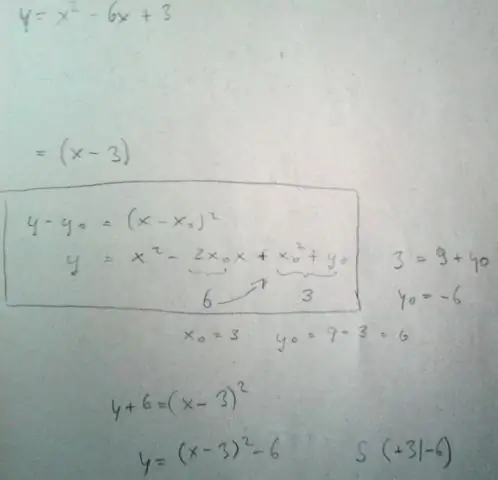
2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35

ΕΝΑ τετραγωνική λειτουργία είναι μία από τη μορφή f(x) = ax² + bx + c, όπου τα a, b και c είναι αριθμοί με a όχι ίσο με μηδέν. Η γραφική παράσταση του α τετραγωνική λειτουργία είναι μια καμπύλη που ονομάζεται παραβολή. Οι παραβολές μπορεί να ανοίγουν προς τα πάνω ή προς τα κάτω και να ποικίλλουν σε "πλάτος" ή "απότομο", αλλά όλες έχουν το ίδιο βασικό σχήμα "U".

Από εδώ, ΤΙ ΕΙΝΑΙ Α σε μορφή κορυφής;

y = a(x – h)² + k, όπου (h, k) είναι το κορυφή . Το «α» στο μορφή κορυφής είναι το ίδιο «α» με. σε y = τσεκούρι² + bx + c (δηλαδή και τα δύο α έχουν ακριβώς την ίδια τιμή). Η πινακίδα στο "a" σας λέει εάν το τετράγωνο ανοίγει ή ανοίγει προς τα κάτω.

πώς προσδιορίζετε ότι μια εξίσωση είναι συνάρτηση; Είναι σχετικά εύκολο να καθορίσει αν μια η εξίσωση είναι συνάρτηση λύνοντας το y. Όταν σας δίνεται ένα εξίσωση και μια συγκεκριμένη τιμή για το x, θα πρέπει να υπάρχει μόνο μία αντίστοιχη τιμή y για αυτήν την τιμή x. Για παράδειγμα, y = x + 1 είναι α λειτουργία γιατί το y θα είναι πάντα ένα μεγαλύτερο από το x.

Με αυτόν τον τρόπο, πώς γράφετε μια εξίσωση για μια παραβολή;

Για παραβολές που ανοίγει πλάγια, η τυπική φόρμα εξίσωση είναι (y - k)^2 = 4p(x - h). Η κορυφή ή η άκρη του μας παραβολή δίνεται από το σημείο (η, κ). Για παραβολές που ανοίγουν πάνω-κάτω, το σημείο εστίασης δίνεται από το (h, k + p). Για παραβολές που ανοίγει προς τα πλάγια, το σημείο εστίασης είναι (h + p, k).

Ποια είναι η τυπική μορφή μιας τετραγωνικής συνάρτησης;

ΕΝΑ τετραγωνική λειτουργία είναι ένα λειτουργία του βαθμού δύο. Η γραφική παράσταση του α τετραγωνική λειτουργία είναι ένα παραβολή . Το Γενικό μορφή τετραγωνικής συνάρτησης είναι f(x)=ax2+bx+c όπου a, b και c είναι πραγματικοί αριθμοί και a≠0. ο τυπική μορφή μιας τετραγωνικής συνάρτησης είναι f(x)=a(x−h)2+k.