
Πίνακας περιεχομένων:
- Συγγραφέας Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:35.
- Τελευταία τροποποίηση 2025-01-22 16:57.
Το τ δοκιμή στατιστική αξία σε δοκιμή αν οι μέσοι όροι είναι διαφορετικοί μπορεί να υπολογιστεί ως εξής: t=mA−mB√S2nA+S2nB. Το S2 είναι ένας εκτιμητής της κοινής διακύμανσης των δύο δειγμάτων. Μπορεί να υπολογιστεί ως εξής: S2=∑(x−mA)2+∑(x−mB)2nA+nB−2.
Απλώς, πώς χρησιμοποιείτε τον τύπο τεστ t;
Φόρμουλα T-Test
- overline{x} = μέσος όρος του πρώτου συνόλου τιμών.
- overline{x}_{2} = μέσος όρος του δεύτερου συνόλου τιμών.
- S_{1} = Τυπική απόκλιση του πρώτου συνόλου τιμών.
- S_{2} = Τυπική απόκλιση του δεύτερου συνόλου τιμών.
- n_{1} = Συνολικός αριθμός τιμών στο πρώτο σετ.
- n_{2} = Συνολικός αριθμός τιμών στο δεύτερο σύνολο.
Εκτός από τα παραπάνω, σε τι χρησιμοποιείται το Τ τεστ; ΕΝΑ t - δοκιμή είναι ένας τύπος επαγωγικής στατιστικής συνηθισμένος να καθορίσουν εάν υπάρχει σημαντική διαφορά μεταξύ των μέσων δύο ομάδων, η οποία μπορεί να σχετίζεται σε ορισμένα χαρακτηριστικά. ΕΝΑ t - δοκιμή είναι που χρησιμοποιείται ως μια υπόθεση δοκιμή εργαλείο, το οποίο επιτρέπει δοκιμή μιας υπόθεσης που ισχύει για έναν πληθυσμό.
Οι άνθρωποι ρωτούν επίσης, πώς υπολογίζετε ένα δείγμα t test;
ο ένα δείγμα t τεστ συγκρίνει τον μέσο όρο σας δείγμα δεδομένα σε μια γνωστή τιμή. Για παράδειγμα , μπορεί να θέλετε να μάθετε πώς σας δείγμα ο μέσος όρος σε σύγκριση με τον μέσο όρο του πληθυσμού.
Παράδειγμα δοκιμής ενός δείγματος Τ
- Ο μέσος όρος του δείγματος (x¯).
- Ο πληθυσμιακός μέσος όρος(μ).
- Το δείγμα τυπικής απόκλισης = 15 $.
- Αριθμός παρατηρήσεων(n) = 25.
Τι είναι το τεστ AF;
Ένα Φ - δοκιμή είναι οποιαδήποτε στατιστική δοκιμή στο οποίο το δοκιμή στατιστική έχει ένα Φ -κατανομή κάτω από τη μηδενική υπόθεση. Χρησιμοποιείται συχνότερα κατά τη σύγκριση στατιστικών μοντέλων που έχουν προσαρμοστεί σε ένα σύνολο δεδομένων, προκειμένου να προσδιοριστεί το μοντέλο που ταιριάζει καλύτερα στον πληθυσμό από τον οποίο ελήφθησαν δείγματα των δεδομένων.
Συνιστάται:
Ποια είναι η εμπειρική φόρμουλα για την καφεΐνη;
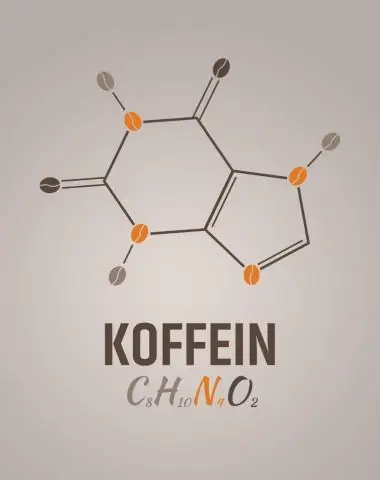
2 Απαντήσεις. Το C8H10N4O2 είναι ο μοριακός τύπος για την καφεΐνη
Ποια είναι η φόρμουλα για την απόδοση μετασχηματισμού;
Μπορεί να υπολογιστεί διαιρώντας τον αριθμό των επιτυχημένων μετασχηματισμών με την ποσότητα του DNA που χρησιμοποιείται κατά τη διάρκεια μιας διαδικασίας μετασχηματισμού
Ποια είναι η δοκιμή δείκτη για νουκλεϊκά οξέα;

Το τεστ διφαινυλαμίνης (Dische) χρησιμοποιείται για τον προσδιορισμό της παρουσίας νουκλεϊκών οξέων. Η παρουσία DNA θα μετατρέψει ένα διαυγές διάλυμα μπλε. Όσο περισσότερο υπάρχει DNA τόσο πιο σκούρο είναι το χρώμα. Ένα άλλο νουκλεϊκό οξύ, το RNA, θα γίνει πράσινο
Ποια είναι η φόρμουλα για το Disilicon Hexabromide;

Disilicon Hexabromide Si2Br6 Molecular Weight -- EndMemo
Ποια είναι η φόρμουλα για το βρωμιούχο χρώμιο II;

Χημικός τύπος: CrBr2
