Βίντεο: Τι είναι ένα παράδειγμα ρητού αριθμού που δεν είναι ακέραιος αριθμός;
2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35
ΕΝΑ λογικός ” αριθμός είναι η αναλογία μεταξύ δύο ακεραίων. Για παράδειγμα , είναι τα ακόλουθα ρητοί αριθμοί , και κανένα από αυτά δεν είναι ακέραιος: 1 / 2. 2 / 3.
Επίσης το ερώτημα είναι, τι είναι ένας ρητός αριθμός που δεν είναι ακέραιος αριθμός;
Όλοι οι αρνητικοί ακέραιοι είναι ρητοί αριθμοί αλλά αυτά είναι όχι ακέραιους αριθμούς . Για παράδειγμα -3 είναι α ρητός αριθμός (μπορεί να εκφραστεί ως -3/1), αλλά είναι όχι ακέραιος αριθμός . Τα κλάσματα όπως 1/2, -3/4, 22/7 κ.λπ.
Δεύτερον, το αρνητικό 3 είναι ρητός αριθμός; − Το 3 είναι αρνητικό άρα δεν είναι φυσικό ή σύνολο αριθμός . Ρητοί αριθμοί είναι αριθμοί που μπορεί να εκφραστεί ως κλάσμα ή λόγος δύο ακεραίων. Ρητοί αριθμοί συμβολίζονται Q. Από − 3 μπορεί να γραφτεί ως − 3 1, θα μπορούσε να υποστηριχθεί ότι − 3 είναι επίσης ένα πραγματικό αριθμός.
Δεύτερον, τι είναι ένας ρητός αριθμός που είναι ακέραιος αριθμός;
Κάθε ολόκληρος ο αριθμός είναι ένα ρητός αριθμός : για παράδειγμα, 3=31. Ετσι είναι λογικός . Κάθε ολόκληρος ο αριθμός Το n μπορεί να γραφτεί ως κλάσμα ακεραίων: n=n1. Δεν είμαστε υποχρεωμένοι να το γράψουμε με αυτόν τον τρόπο. πρέπει απλώς να γνωρίζουμε ότι είναι δυνατό να εκφράσουμε κάθε ολόκληρος ο αριθμός ως κλάσμα ακεραίων, και ως εκ τούτου είναι λογικός.
Μπορεί ένας ρητός αριθμός να είναι ακέραιος αλλά όχι ακέραιος;
Σύνολο απο ολόκληροι αριθμοί = {0, 1, 2, 3, 4, …} Ολόκληροι αριθμοί είναι απλά ακέραιοι αριθμοί που είναι μη αρνητικά. Χρησιμοποιώντας τον συμβολισμό συνόλου, εμείς μπορώ πείτε ότι το σύνολο των ακέραιοι αριθμοί είναι ενώ το σύνολο των ολόκληροι αριθμοί είναι βασικά. Επιστρέφοντας λοιπόν στην ερώτηση. Οχι , υπάρχει κανένας ρητός αριθμός που δεν είναι ακέραιος αλλά είναι ένα ολόκληρος ο αριθμός.
Συνιστάται:
Τι είναι φυσικός αριθμός και ακέραιος αριθμός με παράδειγμα;
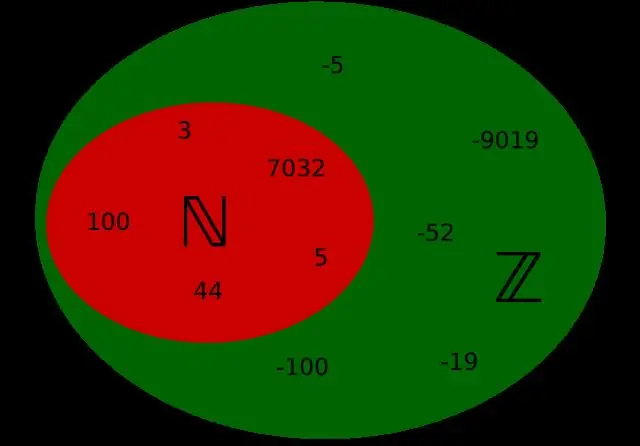
Οι φυσικοί αριθμοί είναι όλοι οι αριθμοί 1, 2, 3, 4… Είναι οι αριθμοί που συνήθως μετράτε και θα συνεχίσουν στο άπειρο. Οι ακέραιοι αριθμοί είναι όλοι φυσικοί αριθμοί συμπεριλαμβανομένου του 0 π.χ. 0, 1, 2, 3, 4… Οι ακέραιοι αριθμοί περιλαμβάνουν όλους τους ακέραιους αριθμούς και το αρνητικό τους αντίστοιχο π.χ.
Ποια είναι η διαφορά μεταξύ του αριθμού Biot και του αριθμού Nusselt;
Η πιο πρόσφατη απάντηση. Ο αριθμός Biot χρησιμοποιεί τη θερμική αγωγιμότητα του σώματος (όχι το υγρό), ενώ ο αριθμός Nusselt χρησιμοποιεί τη θερμική αγωγιμότητα του ρευστού. Οι διαφορές μεταξύ του αριθμού Biot και του αριθμού Nusselt είναι στον ορισμό του συντελεστή μεταφοράς θερμότητας, ο οποίος ορίζεται ως: h=-k (dT/dn)w/(Tw-T0)
Είναι κάθε φυσικός αριθμός ακέραιος αριθμός;
Ναι είναι αλήθεια. Γιατί οι φυσικοί αριθμοί ξεκινούν από το 1 και τελειώνουν στο άπειρο όπου οι ακέραιοι αριθμοί ξεκινούν από το 0 και τελειώνουν στο άπειρο. Το 0 είναι ο μόνος αριθμός που είναι σε ακέραιους αριθμούς αλλά όχι σε φυσικούς αριθμούς. Επομένως, κάθε φυσικός αριθμός είναι ένας ακέραιος αριθμός
Τι είναι ένα καθαρό παράδειγμα φανταστικού αριθμού;
Καθαροί φανταστικοί αριθμοί Ο αριθμός i δεν είναι σε καμία περίπτωση μόνος! Για παράδειγμα, 3 i 3i 3i, i 5 isqrt{5} i5 ?i, τετραγωνική ρίζα του, 5, άκρο τετραγωνική ρίζα και &μείον;12i είναι όλα παραδείγματα καθαρών φανταστικών αριθμών ή αριθμών της μορφής bi bi bi, όπου b είναι ένας μη μηδενικός πραγματικός αριθμός
Τι είναι ένας ακέραιος αριθμός και ένα κλάσμα;
Ναι, ένα κλάσμα μπορεί να είναι ακέραιος αριθμός, για παράδειγμα, Οποιοδήποτε κλάσμα της μορφής a/1 = a, όπου το 'a' είναι ο αριθμητής και το 1 είναι ο παρονομαστής και το 'a' είναι μέλος του συνόλου των ακέραιων αριθμών που ισούται με {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,}