Πίνακας περιεχομένων:
Βίντεο: Πώς αποδεικνύετε έναν χαρταετό στη γεωμετρία συντεταγμένων;
2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35
Εδώ είναι οι δύο μέθοδοι:
- Αν δύο ασύνδετα ζεύγη διαδοχικών πλευρών ενός τετράπλευρου είναι ίσα, τότε είναι χαρταετός (πίσω του χαρταετός ορισμός).
- Αν μία από τις διαγώνιους ενός τετράπλευρου είναι η κάθετη διχοτόμος του άλλου, τότε είναι χαρταετός (αντίστροφη ιδιότητας).
Στη συνέχεια, μπορεί κανείς να αναρωτηθεί, ποια είναι τα χαρακτηριστικά ενός χαρταετού;
Χαρταετός Οι ιδιότητες περιλαμβάνουν (1) δύο ζεύγη διαδοχικών, ομοίων πλευρών, (2) ίσες γωνίες μη κορυφών και (3) κάθετες διαγώνιες. Άλλες σημαντικές ιδιότητες πολυγώνου που πρέπει να γνωρίζετε είναι οι ιδιότητες τραπεζοειδούς, ιδιότητες παραλληλογράμμου, ιδιότητες ρόμβου και ιδιότητες ορθογωνίου και τετραγώνου.
Γνωρίζετε επίσης, είναι ένα ορθογώνιο κάθετο; Όπως μπορείτε να δείτε από τις εικόνες στα αριστερά, οι διαγώνιοι του α ορθογώνιο παραλληλόγραμμο δεν τέμνονται σε ορθή γωνία (δεν είναι κάθετος ). (Εκτός κι αν το ορθογώνιο παραλληλόγραμμο είναι τετράγωνο.) Και οι γωνίες που σχηματίζει η τομή δεν είναι πάντα το ίδιο μέτρο (μέγεθος). Οι απέναντι κεντρικές γωνίες έχουν το ίδιο μέγεθος (είναι ίσες.)
Στη συνέχεια, το ερώτημα είναι, είναι ένας χαρταετός κάθετος;
ΟΡΙΣΜΟΣ: Α χαρταετός είναι ένα τετράπλευρο του οποίου οι τέσσερις πλευρές είναι σχεδιασμένες έτσι ώστε να υπάρχουν δύο διαφορετικά σύνολα γειτονικών, σύμφωνος πλευρές. ΘΕΩΡΗΜΑ: Αν ένα τετράπλευρο είναι χαρταετός , οι διαγώνιοι είναι κάθετος . ΘΕΩΡΗΜΑ: Αν ένα τετράπλευρο είναι χαρταετός , έχει ένα ζεύγος αντίθετων γωνιών σύμφωνος.
Είναι ένα παραλληλόγραμμο παραλληλόγραμμο;
ΕΝΑ ορθογώνιο παραλληλόγραμμο έχει δύο ζεύγη απέναντι πλευρές παράλληλες και τέσσερις ορθές γωνίες. Είναι επίσης ένα παραλληλόγραμμο , αφού έχει δύο ζεύγη παράλληλων πλευρών.
Συνιστάται:
Πώς καλλιεργείτε έναν θάμνο κρεόσωτου από έναν σπόρο;
Η μέθοδος για την καλλιέργεια φυτών κρεόσωτου απαιτεί την εμβάπτιση των σπόρων σε βραστό νερό για να διαπεράσει το βαρύ στρώμα σπόρων. Μουλιάστε τα για μια μέρα και μετά φυτέψτε έναν σπόρο ανά γλάστρα 2 ιντσών. Διατηρήστε τους σπόρους ελαφρώς υγρούς μέχρι να βλαστήσουν. Στη συνέχεια, μετακινήστε τα σε μια ζεστή, ηλιόλουστη τοποθεσία και αναπτύξτε τα μέχρι να δημιουργηθεί ένα πλήρες σύνολο ριζών
Πώς βρίσκετε το Preimage στη γεωμετρία;
Η εικόνα T(V) ορίζεται ως το σύνολο {k | k=T(v) για κάποιο v στο V}. Άρα x=T(y) όπου το y είναι στοιχείο του T^-1(S). Το preimage του S είναι το σύνολο {m | Το T(m) είναι σε S}. Έτσι το T(y) είναι στο S, άρα αφού x=T(y), έχουμε ότι το x είναι στο S
Πώς γράφετε έναν κανόνα συντεταγμένων για μια περιστροφή;
Για να γράψετε έναν κανόνα για αυτήν την περιστροφή θα γράφατε: R270; (x,y)=(&μείον;y,x). Κανόνας σημειογραφίας Ένας κανόνας σημειογραφίας έχει την ακόλουθη μορφή R180; A → O = R180; (x,y) → (&μείον x,&μίον;y) και σας λέει ότι η εικόνα A έχει περιστραφεί γύρω από την αρχή και και οι δύο συντεταγμένες x και y πολλαπλασιάζονται με -1
Πώς χαρακτηρίζετε τα σημεία στη γεωμετρία;
Ένα σημείο είναι η πιο θεμελιώδης γεωμετρία αντικειμένου. Αντιπροσωπεύεται από μια τελεία και ονομάζεται με κεφαλαίο. Ένα σημείο αντιπροσωπεύει μόνο θέση. έχει μηδενικό μέγεθος (δηλαδή μηδέν μήκος, μηδέν πλάτος και μηδέν ύψος). Το σχήμα 1 απεικονίζει το σημείο C, το σημείο M και το σημείο Q
Πώς κατασκευάζετε ένα επίπεδο συντεταγμένων στη γεωμετρία;
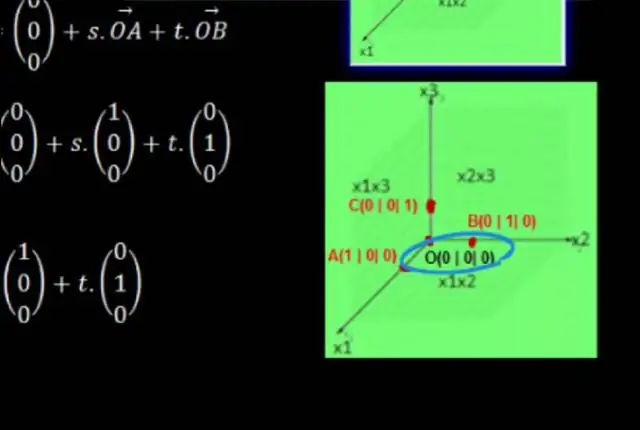
Για να δημιουργήσουμε ένα επίπεδο συντεταγμένων, ακολουθούμε τα εξής βήματα: Σχεδιάστε δύο αριθμητικές ευθείες κάθετες μεταξύ τους, που τέμνονται στο σημείο 0 και στις δύο ευθείες. Επισημάνετε την οριζόντια αριθμητική γραμμή ως άξονα x και την κάθετη αριθμητική γραμμή ως άξονα y