Τι είναι οι σημειακές ευθείες και τα επίπεδα;

2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35

ΕΝΑ σημείο στη γεωμετρία είναι μια τοποθεσία. Δεν έχει μέγεθος, δηλαδή πλάτος, μήκος και βάθος. ΕΝΑ σημείο εμφανίζεται με μια τελεία. ΕΝΑ γραμμή ορίζεται ως α γραμμή του σημεία που εκτείνεται άπειρα σε δύο κατευθύνσεις. ΕΝΑ επίπεδο ονομάζεται από τρεις σημεία στο επίπεδο που δεν είναι στο ίδιο γραμμή.

Συνεπώς, γιατί οι ευθείες και τα επίπεδα σημεία είναι απροσδιόριστοι όροι;

Στη Γεωμετρία, ορίζουμε α σημείο ως τοποθεσία και χωρίς μέγεθος. ΕΝΑ γραμμή ορίζεται ως κάτι που εκτείνεται άπειρα προς κάθε κατεύθυνση αλλά δεν έχει πλάτος και είναι μονοδιάστατο ενώ α επίπεδο εκτείνεται άπειρα σε δύο διαστάσεις. Υπάρχουν τρία απροσδιόριστους όρους στη γεωμετρία. ΕΝΑ σημείο δεν έχει μέγεθος? έχει μόνο τοποθεσία.

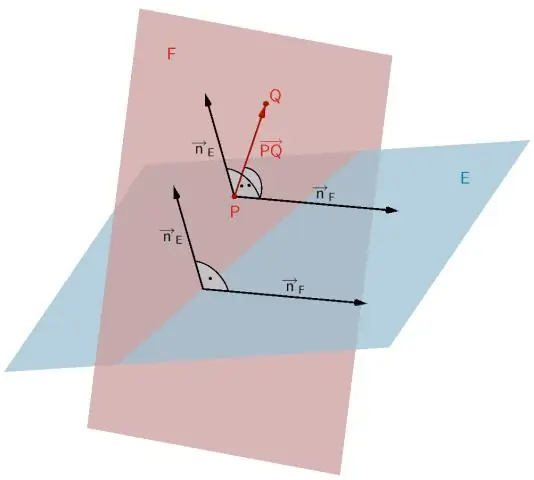
Επιπλέον, πόσα επίπεδα περιέχουν κάθε ευθεία και σημείο; Για παράδειγμα, εάν τα τρία σημεία είναι Α, Β και Γ στο διάγραμμά σας, τότε υπάρχουν άπειρα πολλά επίπεδα που περιέχουν τα σημεία. έχω εικονογραφήσει δύο τέτοια επίπεδα σε ροζ χρώμα στα παρακάτω διαγράμματα. Το τελευταίο σημείο είναι ότι αν τα τρία σημεία δεν βρίσκονται σε μια γραμμή, τότε υπάρχει ακριβώς ένα αεροπλάνο που περιέχει τα σημεία.

Στη συνέχεια, το ερώτημα είναι, ποια είναι μερικά παραδείγματα σημειακών γραμμών και επιπέδων στον πραγματικό κόσμο;

Παραδείγματα μπορεί να είναι τρίγωνα, τετράγωνα, ορθογώνια, γραμμές , κύκλους, σημεία , πεντάγωνα, πινακίδες στοπ (οκτάγωνα), κουτιά (πρίσματα ή ζάρια (κύβοι). Παραδείγματα του α επίπεδο θα ήταν: μια επιφάνεια εργασίας, ο πίνακας κιμωλίας/ασπροπίνακας, ένα κομμάτι χαρτί, μια οθόνη τηλεόρασης, παράθυρο, τοίχος ή μια πόρτα.

Πόσους βαθμούς χρειάζεστε για να φτιάξετε ένα αεροπλάνο;

Σε έναν Ευκλείδειο χώρο οποιουδήποτε αριθμού διαστάσεων, ένα επίπεδο προσδιορίζεται μοναδικά από οποιοδήποτε από τα ακόλουθα: Τρία μη γραμμικά σημεία (σημεία όχι σε μία γραμμή). Μια γραμμή και ένα σημείο όχι σε αυτή τη γραμμή. Δύο ευδιάκριτες αλλά τεμνόμενες γραμμές.