
- Συγγραφέας Miles Stephen [email protected].
- Public 2023-12-15 23:35.
- Τελευταία τροποποίηση 2025-01-22 16:57.
Για να βρείτε το περιοχή αυτού του τετραγώνου, πολλαπλασιάζουμε το μήκος της πλευράς από μόνο του ή το τετραγωνίζουμε. ο περιοχή , 4x2, είναι γινόμενο ενός αριθμού (4) και μιας μεταβλητής με εκθέτη ακέραιου αριθμού (x2). Με άλλα λόγια, είναι ένα μονώνυμος , πολύ. Άρα το αποτέλεσμα του πολλαπλασιασμού δύο μονώνυμα είναι-άλλος μονώνυμος !
Επιπλέον, πώς πολλαπλασιάζετε και διαιρείτε Μονώνυμα;
Προς το πολλαπλασιάζω ένα μονώνυμος με γνωστό αριθμό, απλά πολλαπλασιάζω ο συντελεστής με τον αριθμό. Προς το πολλαπλασιάζω ένα μονώνυμος από μια μεταβλητή, απλά πολλαπλασιάζω η μεταβλητή από την άλλη μεταβλητή? αυτό συχνά οδηγεί σε έναν εκθέτη. Προς το διαιρέστε ένα μονώνυμος με γνωστό αριθμό, απλά διαιρέστε ο συντελεστής με τον εν λόγω αριθμό.
Γνωρίζετε επίσης, το τετράγωνο είναι Μονώνυμο; Πολλαπλασιάζοντας Μονωνύμων Σκεφτείτε α τετράγωνο του οποίου το μήκος είναι 2x. Για να βρείτε την περιοχή αυτού τετράγωνο , πολλαπλασιάζουμε το μήκος της πλευράς από μόνο του, ή τετράγωνο το. Η περιοχή, 4x2, είναι γινόμενο ενός αριθμού (4) και μιας μεταβλητής με εκθέτη ακέραιου αριθμού (x2). Με άλλα λόγια, είναι ένα μονώνυμος , πολύ.
Ομοίως, τι είναι οι συντελεστές;
Στα μαθηματικά, α συντελεστής είναι ένας πολλαπλασιαστικός παράγοντας σε κάποιο όρο ενός πολυωνύμου, μιας σειράς ή οποιασδήποτε έκφρασης. είναι συνήθως ένας αριθμός, αλλά μπορεί να είναι οποιαδήποτε έκφραση. Για παράδειγμα, εάν το y θεωρείται ως παράμετρος στην παραπάνω παράσταση, το συντελεστής του x είναι −3y και η σταθερά συντελεστής είναι 1,5 + y.
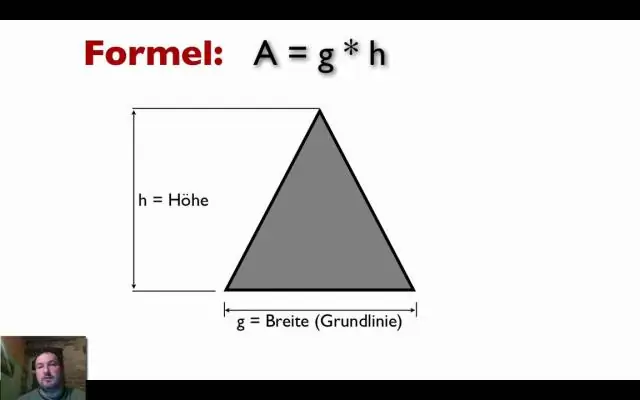
Πώς βρίσκετε το εμβαδόν ενός τριγώνου;
Προς το εύρημα ο περιοχή του α τρίγωνο , πολλαπλασιάστε τη βάση με το ύψος και μετά διαιρέστε με το 2. Η διαίρεση με το 2 προέρχεται από το γεγονός ότι ένα παραλληλόγραμμο μπορεί να χωριστεί σε 2 τρίγωνα . Για παράδειγμα, στο διάγραμμα στα αριστερά, το περιοχή από το καθένα τρίγωνο ισούται με το μισό του περιοχή του παραλληλογράμμου.
Συνιστάται:
Ποια είναι η διαφορά μεταξύ ενός ultramafic, ενός mafic, ενός intermediate και ενός felsic rock;

Σε ένα ευρέως αποδεκτό σύστημα ταξινόμησης περιεκτικότητας σε πυρίτιο, τα πετρώματα με περισσότερο από 65 τοις εκατό πυρίτιο ονομάζονται felsic. Αυτά με μεταξύ 55 και 65 τοις εκατό πυρίτιο είναι ενδιάμεσα. Αυτά με μεταξύ 45 και 55 τοις εκατό πυρίτιο είναι μαφικά. και εκείνοι με λιγότερο από 45 τοις εκατό είναι υπερμαφικοί
Πώς βρίσκετε το εμβαδόν ενός σχήματος σε τετράγωνες μονάδες;

Η περιοχή μετριέται σε «τετράγωνες» μονάδες. Το εμβαδόν μιας φιγούρας είναι ο αριθμός των τετραγώνων που απαιτούνται για να την καλύψουν πλήρως, όπως τα πλακάκια σε ένα πάτωμα. Εμβαδόν τετραγώνου = πλευρά επί πλευρά. Δεδομένου ότι κάθε πλευρά ενός τετραγώνου είναι η ίδια, μπορεί απλώς να είναι το μήκος μιας πλευράς στο τετράγωνο
Πώς βρίσκετε τις διαστάσεις όταν δίνεται το εμβαδόν και η περίμετρος;
Εύρεση μήκους και πλάτους όταν γνωρίζετε εμβαδόν και περίμετρο Εάν τυχαίνει να γνωρίζετε την απόσταση γύρω από το ορθογώνιο, που είναι η περίμετρός του, μπορείτε να λύσετε ένα ζεύγος εξισώσεων για το L και το W. Η πρώτη εξίσωση είναι ότι για το εμβαδόν, A = L ⋅ W, και το δεύτερο είναι ότι για την περίμετρο, P = 2L + 2W
Πώς βρίσκετε το εμβαδόν και την περίμετρο στα μαθηματικά;

Ο τύπος για την περίμετρο ενός ορθογωνίου γράφεται συχνά ως P = 2l + 2w, όπου l είναι το μήκος του ορθογωνίου και w είναι το πλάτος του ορθογωνίου. Το εμβαδόν ενός δισδιάστατου σχήματος περιγράφει το μέγεθος της επιφάνειας που καλύπτει το σχήμα. Μετράτε το εμβαδόν σε τετράγωνες μονάδες σταθερού μεγέθους
Πώς βρίσκετε το εμβαδόν βάσης ενός τριγωνικού πρίσματος;

Ένα τριγωνικό πρίσμα έχει τρεις ορθογώνιες πλευρές και δύο τριγωνικές όψεις. Για να βρείτε το εμβαδόν των ορθογώνιων πλευρών, χρησιμοποιήστε τον τύπο A = lw, όπου A = εμβαδόν, l = μήκος και h = ύψος. Για να βρείτε το εμβαδόν των τριγωνικών όψεων, χρησιμοποιήστε τον τύπο A = 1/2bh, όπου A = εμβαδόν, b = βάση και h = ύψος
