Πίνακας περιεχομένων:
Βίντεο: Ποια είναι μερικά πραγματικά παραδείγματα γραμμικών συναρτήσεων;
2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35
Αρχική απάντηση: Θα μπορούσε κάποιος να μου δώσει ένα παράδειγμα του μια γραμμική συνάρτηση πραγματική ζωή κατάσταση? Γραμμικές συναρτήσεις συμβεί όποτε το έχετε ένα σταθερό ρυθμό μεταβολής.
Παραδείγματα πραγματικής ζωής είναι:
- Εύρεση ρεύματος που καταναλώθηκε την ημέρα 1, 2, 3…
- Παίρνετε ένα αυτοκίνητο προς ενοικίαση.
- Οδηγείς ένα αυτοκίνητο στο ο ταχύτητα 60 χλμ/ώρα.
Λαμβάνοντας υπόψη αυτό, ποιο είναι ένα πραγματικό παράδειγμα μιας γραμμικής συνάρτησης;
Παράδειγμα : Γράφημα τη γραμμή που δείχνει την ταχύτητα Η κλίση ήταν 5 μίλια την ώρα και δεδομένου ότι το σημείο εκκίνησης ήταν στο (0, 0), η τομή y είναι 0. Ο τελικός μας λοιπόν λειτουργία είναι y=5x y = 5 x. Γράφημα απόστασης και χρόνου: Η γραφική παράσταση του y=5x y = 5 x. Οι δύο μεταβλητές είναι ο χρόνος (x) και η απόσταση (y).
Επιπλέον, τι είναι ένα παράδειγμα γραμμικής εξίσωσης; Παράδειγμα : y = 2x + 1 είναι α γραμμική εξίσωση : Η γραφική παράσταση του y = 2x+1 είναι ευθεία γραμμή. Όταν το x αυξάνεται, το y αυξάνεται δύο φορές πιο γρήγορα, οπότε χρειαζόμαστε 2x. Όταν το x είναι 0, το y είναι ήδη 1.
Ομοίως, οι άνθρωποι ρωτούν, πού χρησιμοποιούμε τις συναρτήσεις στην πραγματική ζωή;
Ακολουθούν μερικά παραδείγματα:
- Περιφέρεια κύκλου - Η περιφέρεια ενός κύκλου είναι συνάρτηση της διαμέτρου του.
- Μια σκιά - Το μήκος της σκιάς ενός ατόμου κατά μήκος του δαπέδου είναι συνάρτηση του ύψους του.
- Οδήγηση αυτοκινήτου - Όταν οδηγείτε ένα αυτοκίνητο, η τοποθεσία σας είναι συνάρτηση του χρόνου.
Πώς χρησιμοποιούνται οι γραμμικές ανισότητες στην πραγματική ζωή;
Ένα σύστημα από γραμμικές ανισότητες είναι συχνά μεταχειρισμένος για να προσδιορίσετε την καλύτερη λύση σε ένα πρόβλημα. Αυτή η λύση θα μπορούσε να είναι τόσο απλή όσο ο καθορισμός του πόσα από ένα προϊόν θα πρέπει να παραχθεί για να μεγιστοποιηθεί το κέρδος ή τόσο περίπλοκη όσο ο καθορισμός του σωστού συνδυασμού φαρμάκων που θα δώσει σε έναν ασθενή.
Συνιστάται:
Ποια είναι μερικά παραδείγματα κώνου;
Ο κώνος είναι μια τρισδιάστατη γεωμετρική δομή που λεπταίνει ομαλά από την επίπεδη βάση σε ένα σημείο που ονομάζεται κορυφή ή κορυφή. Χωνάκια παγωτού. Αυτοί είναι οι πιο γνωστοί κώνοι που γνωρίζει κάθε παιδί σε όλο τον κόσμο. Καπέλα γενεθλίων. Κώνοι κυκλοφορίας. Χωνί. Teepee/Tipi. Πύργος του Κάστρου. Temple Top. Μεγάφωνα
Ποια είναι μερικά παραδείγματα αλλοτρόπων;
Παραδείγματα αλλοτροπών Για να συνεχίσουμε το παράδειγμα άνθρακα, το ινδιάμαντο, τα άτομα άνθρακα συνδέονται για να σχηματίσουν μια τετραεδρική πλέξη. Στον γραφίτη, τα άτομα συνδέονται για να σχηματίσουν φύλλα εξαγωνικού πλέγματος. Άλλα αλλότροπα του άνθρακα περιλαμβάνουν το γραφένιο και τα φουλερένια. Το O2 και το όζον, O3, είναι αλλότροπα του οξυγόνου
Πώς είναι παρόμοια η επίλυση γραμμικών ανισώσεων και γραμμικών εξισώσεων;
Η επίλυση γραμμικών ανισώσεων είναι πολύ παρόμοια με την επίλυση γραμμικών εξισώσεων. Η κύρια διαφορά είναι ότι αντιστρέφετε το σύμβολο της ανισότητας όταν διαιρείτε ή πολλαπλασιάζετε με έναν αρνητικό αριθμό. Η γραφική παράσταση γραμμικών ανισοτήτων έχει μερικές ακόμη διαφορές. Το τμήμα που είναι σκιασμένο περιλαμβάνει τις τιμές όπου η γραμμική ανισότητα είναι αληθής
Ποιος είναι ο σκοπός των γραμμικών συναρτήσεων;
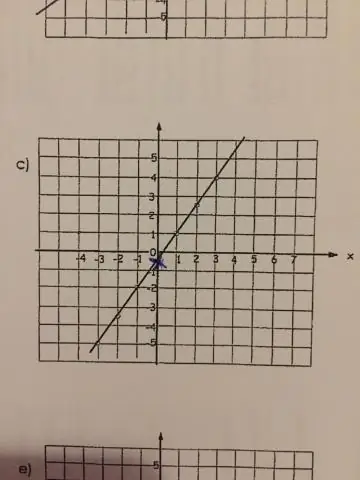
Γραμμική συνάρτηση είναι κάθε συνάρτηση που απεικονίζει μια ευθεία γραμμή. Αυτό σημαίνει μαθηματικά ότι η συνάρτηση έχει είτε μία είτε δύο μεταβλητές χωρίς εκθέτες ή δυνάμεις. Εάν η συνάρτηση έχει περισσότερες μεταβλητές, οι μεταβλητές πρέπει να είναι σταθερές ή γνωστές μεταβλητές για να παραμείνει η συνάρτηση γραμμική συνάρτηση
Ποια είναι η διαφορά μεταξύ της μικροεξέλιξης και της μακροεξέλιξης Ποια είναι μερικά παραδείγματα από το καθένα;
Μικροεξέλιξη εναντίον Μακροεξέλιξης. Παραδείγματα τέτοιων μικροεξελικτικών αλλαγών θα περιλαμβάνουν μια αλλαγή στο χρώμα ή το μέγεθος ενός είδους. Η μακροεξέλιξη, αντίθετα, χρησιμοποιείται για να αναφέρεται σε αλλαγές σε οργανισμούς που είναι αρκετά σημαντικές ώστε, με την πάροδο του χρόνου, οι νεότεροι οργανισμοί να θεωρούνται εντελώς νέο είδος