Βίντεο: Πότε πρέπει να χρησιμοποιείτε τη συσχέτιση και πότε να χρησιμοποιείτε απλή γραμμική παλινδρόμηση;
2024 Συγγραφέας: Miles Stephen | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:35
Οπισθοδρόμηση είναι πρωτίστως συνηθισμένος κατασκευή μοντέλων/εξισώσεων προς το προβλέψτε μια βασική απάντηση, Y, από ένα σύνολο μεταβλητών πρόβλεψης (X). Συσχέτιση είναι πρωτίστως συνηθισμένος συνοψίστε γρήγορα και συνοπτικά την κατεύθυνση και τη δύναμη των σχέσεων μεταξύ ενός συνόλου 2 ή περισσότερων αριθμητικών μεταβλητών.
Επίσης, πρέπει να γνωρίζετε, πότε πρέπει να χρησιμοποιήσετε γραμμική παλινδρόμηση;
Τρεις κύριοι χρήσεις Για οπισθοδρόμηση Η ανάλυση είναι (1) ο προσδιορισμός της ισχύος των προβλέψεων, (2) η πρόβλεψη ενός αποτελέσματος και (3) η πρόβλεψη τάσης. Πρώτον, το οπισθοδρόμηση μπορεί να χρησιμοποιηθεί προς το Προσδιορίστε την ισχύ της επίδρασης που ασκούν οι ανεξάρτητες μεταβλητές σε μια εξαρτημένη μεταβλητή.
Επίσης, πότε πρέπει να χρησιμοποιείται η συσχέτιση; Συσχέτιση είναι μεταχειρισμένος να περιγράψει τη γραμμική σχέση μεταξύ δύο συνεχών μεταβλητών (π.χ. ύψος και βάρος). Γενικά, συσχέτιση τείνει να είναι μεταχειρισμένος όταν δεν υπάρχει προσδιορισμένη μεταβλητή απόκρισης. Μετρά την ισχύ (ποιοτικά) και την κατεύθυνση της γραμμικής σχέσης μεταξύ δύο ή περισσότερων μεταβλητών.
Μπορεί επίσης να ρωτήσει κανείς, ποια είναι η διαφορά μεταξύ της απλής γραμμικής παλινδρόμησης και της συσχέτισης;
Οπισθοδρόμηση περιγράφει πώς μια ανεξάρτητη μεταβλητή σχετίζεται αριθμητικά με την εξαρτημένη μεταβλητή. Συσχέτιση χρησιμοποιείται για να αναπαραστήσει το γραμμικός σχέση μεταξύ δύο μεταβλητές. Αντιθέτως, οπισθοδρόμηση χρησιμοποιείται για να ταιριάζει στην καλύτερη γραμμή και να υπολογίζει μια μεταβλητή με βάση του άλλη μεταβλητή.
Τι ισχύει για τη συσχέτιση Pearson και την απλή γραμμική παλινδρόμηση;
Συσχέτιση Pearson και Γραμμικής παλινδρόμησης . ΕΝΑ συσχέτιση Η ανάλυση παρέχει πληροφορίες για τη δύναμη και την κατεύθυνση του γραμμικός σχέση μεταξύ δύο μεταβλητών, ενώ α απλή γραμμική ανάλυση παλινδρόμησης εκτιμά παραμέτρους σε α γραμμικός εξίσωση που μπορεί να χρησιμοποιηθεί για την πρόβλεψη τιμών μιας μεταβλητής με βάση την άλλη
Συνιστάται:
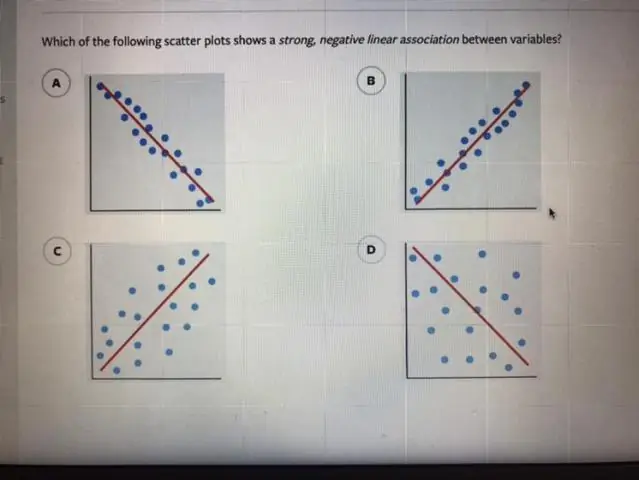
Τι είναι μια αρνητική γραμμική συσχέτιση;
Μια αρνητική συσχέτιση σημαίνει ότι υπάρχει μια αντίστροφη σχέση μεταξύ δύο μεταβλητών - όταν μια μεταβλητή μειώνεται, η άλλη αυξάνεται
Τι σημαίνει γραμμική συσχέτιση;
Μια γραμμική σχέση (ή γραμμική σχέση) είναι ένας στατιστικός όρος που χρησιμοποιείται για να περιγράψει μια ευθύγραμμη σχέση μεταξύ μιας μεταβλητής και μιας σταθεράς
Τι είναι η γραμμική παλινδρόμηση στον προγραμματισμό R;
Η γραμμική παλινδρόμηση χρησιμοποιείται για την πρόβλεψη της τιμής μιας συνεχούς μεταβλητής Υ με βάση μία ή περισσότερες μεταβλητές πρόβλεψης εισόδου X. Ο στόχος είναι να δημιουργηθεί ένας μαθηματικός τύπος μεταξύ της μεταβλητής απόκρισης (Y) και των μεταβλητών πρόβλεψης (Xs). Μπορείτε να χρησιμοποιήσετε αυτόν τον τύπο για να προβλέψετε το Y, όταν είναι γνωστές μόνο οι τιμές X
Πώς υπολογίζετε τη μη γραμμική παλινδρόμηση;
Εάν το μοντέλο σας χρησιμοποιεί μια εξίσωση με τη μορφή Y = a0 + b1X1, είναι ένα μοντέλο γραμμικής παλινδρόμησης. Αν όχι, είναι μη γραμμικό. Y = f(X,β) + ε X = διάνυσμα p προβλέψεων, β = διάνυσμα k παραμέτρων, f(-) = γνωστή συνάρτηση παλινδρόμησης, ε = όρος σφάλματος
Σε τι χρησιμοποιείται η μη γραμμική παλινδρόμηση;
Η μη γραμμική παλινδρόμηση είναι μια μορφή ανάλυσης παλινδρόμησης στην οποία τα δεδομένα προσαρμόζονται σε ένα μοντέλο και στη συνέχεια εκφράζονται ως μαθηματική συνάρτηση. Η μη γραμμική παλινδρόμηση χρησιμοποιεί λογαριθμικές συναρτήσεις, τριγωνομετρικές συναρτήσεις, εκθετικές συναρτήσεις, συναρτήσεις ισχύος, καμπύλες Lorenz, συναρτήσεις Gauss και άλλες μεθόδους προσαρμογής